大家或许还记得 Quake III 里面的一段有如天书般的代码,其中用到的神秘常量 0x5F3759DF 究竟是怎么一回事,着实让不少人伤透了脑筋。今天,我见到了一段同样诡异的代码。
下面这个位运算小技巧可以迅速给出一个数的二进制表达中末尾有多少个 0 。比如, 123 456 的二进制表达是 1 11100010 01000000 ,因此这个程序给出的结果就是 6 。
unsigned int v; // find the number of trailing zeros in 32-bit v
int r; // result goes here
static const int MultiplyDeBruijnBitPosition[32] =
{
0, 1, 28, 2, 29, 14, 24, 3, 30, 22, 20, 15, 25, 17, 4, 8,
31, 27, 13, 23, 21, 19, 16, 7, 26, 12, 18, 6, 11, 5, 10, 9
};
r = MultiplyDeBruijnBitPosition[((uint32_t)((v & -v) * 0x077CB531U)) >> 27];
熟悉位运算的朋友们可以认出, v & -v 的作用就是取出右起连续的 0 以及首次出现的 1 。当 v = 123 456 时, v & -v 就等于 64 ,即二进制的 1000000 。怪就怪在,这个 0x077CB531 是怎么回事?数组 MultiplyDeBruijnBitPosition 又是什么玩意儿呢?
这还得从 0x077CB531 本身的一个性质开始说起。把这个常数写成 32 位二进制,可以得到
00000111011111001011010100110001
这个 01 串有一个无比牛 B 的地方:如果把它看作是循环的,它正好包含了全部 32 种可能的 5 位 01 串,既无重复,又无遗漏!其实,这样的 01 串并不稀奇,因为构造这样的 01 串完全等价于寻找一个有向图中的 Euler 回路。如下图,构造一个包含 16 个顶点的图,顶点分别命名为 0000, 0001, 0010, …, 1111 。如果某个点的后 3 位,正好等于另一个点的前 3 位,就画一条从前者出发指向后者的箭头。也就是说,只要两个顶点上的数满足 abcd 和 bcde 的关系( a 、 b 、 c 、 d 、 e 可能代表相同的数字),就从 abcd 出发,连一条到 bcde 的路,这条路就记作 abcde 。注意,有些点之间是可以相互到达的(比如 1010 和 0101 ),有些点甚至有一条到达自己的路(比如 0000 )。
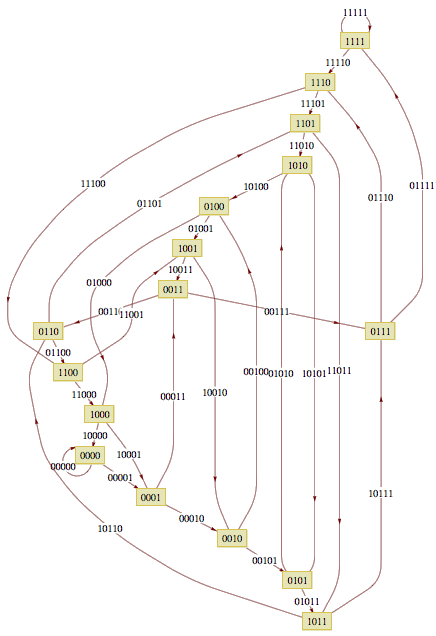
构造一个字符串使其包含所有可能的 5 位 01 子串,其实就相当于沿着箭头在上图中游走的过程。不妨假设字符串以 0000 开头。如果下一个数字是 1 ,那么 00001 这个子串就被包含了,同时最新的 4 位数就变成了 0001 ;但若下一个数字还是 0 ,那么 00000 就被包含了进来,最新的 4 个数仍然是 0000 。从图上看,这无非是一个从 0000 点出发走了哪条路的问题:你是选择了沿 00001 这条路走到了 0001 这个点,还是沿着 00000 这条路走回了 0000 这个点。同理,每添加一个数字,就相当于沿着某条路走到了一个新的点,路上所写的 5 位数就是刚被考虑到的 5 位数。我们的目的便是既无重复又无遗漏地遍历所有的路。显然图中的每个顶点入度和出度都是 2 ,因此这个图一定存在 Euler 回路,我们便能轻易构造出一个满足要求的 01 串了。这样的 01 串就叫做 De Bruijn 序列。
De Bruijn 序列在这里究竟有什么用呢?它的用途其实很简单,就是为 32 种不同的情况提供了一个唯一索引。比方说, 1000000 后面有 6 个 0 ,将 1000000 乘以 0x077CB531 ,就得到
00000111011111001011010100110001
-> 11011111001011010100110001000000
相当于把 De Bruijn 序列左移了 6 位。再把这个数右移 27 位,就相当于提取出了这个数的头 5 位:
11011111001011010100110001000000
-> 11011
由于 De Bruijn 序列的性质,因此当输入数字的末尾 0 个数不同时,最后得到的这个 5 位数也不同。而数组 MultiplyDeBruijnBitPosition 则相当于一个字典的功能。 11011 转回十进制是 27 ,于是我们查一查 MultiplyDeBruijnBitPosition[27] ,程序即返回 6 。
注意到当输入数字的末尾 0 个数超过 27 个时,程序也是正确的,因为左移时低位正好是用 0 填充的。
这段神一般的代码取自 http://graphics.stanford.edu/~seander/bithacks.html ,欢迎大家前去围观。