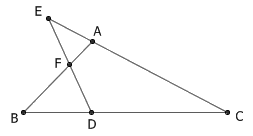
Menelaus 定理是平面几何中用于判断三点共线的一个常用定理。在 △ABC 中,点 D 、 E 、 F 分别在 BC 、 AC 、 AB 所在直线上,若 D 、 E 、 F 三点共线,则有 AF/BF · BD/CD · CE/AE = 1 。 Menelaus 定理的证明方法有很多,今天我见到了我所见过的证明方法中最帅的一种,它解决了之前很多证明方法缺乏对称性的问题,完美展示了几何命题中的对称之美。
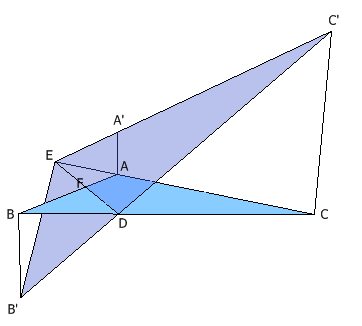
过 DEF 所在直线作一个新的平面(没错,辅助线做到三维空间中去了)。分别过 A 、 B 、 C 作原平面的垂线,与新的平面交于点 A’ 、 B’ 、 C’ 。于是,我们有:
AA’ / BB’ = AF / BF
BB’ / CC’ = BD / CD
CC’ / AA’ = CE / AE
三式乘在一块儿,结论得证。