
定理:平面上有三个圆,每一对圆的外公切线交于一点,则三个交点共线。
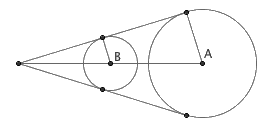
证明 1 :容易证明,对于两个圆 ⊙A 和 ⊙B ,外公切线的交点到它们的圆心的距离与它们各自的半径成正比。也就是说,如果 ⊙A 的质量是 1/ra ,⊙B 的质量是 -1/rb ,那么由杠杆原理(考虑朝向屏幕内部的大小为 1/ra 的重力,以及由于“反重力”得到的朝向屏幕外的大小为 1/rb 的力),这两个物体的重心就位于它们的外公切线的交点处。
现在,考虑平面上的三个圆 ⊙A 、 ⊙B 、 ⊙C ,它们的质量都与各自的半径成反比。考虑系统 {ma , -mb} ,它的重心在 ⊙A 、 ⊙B 外公切线的交点处;考虑另一个系统 {mb , -mc} ,它的重心则在 ⊙B 、 ⊙C 外公切线的交点处。最后,考虑系统 {ma , -mc} ,它的重心应该在 ⊙A 、 ⊙C 外公切线的交点处。而最后这个系统其实是前两个系统合成的结果,它的重心显然应该和前两个系统的重心共线。
证明 2 :把平面上的三个圆想像成空间中的三个球,每一对圆的外公切线就成了这对球所确定的圆锥的母线。我们要证明的就是,这三个圆锥的顶点共线。
考虑三个球的一个公切面,显然它和这三个圆锥的侧面也都相切,因此三个圆锥的顶点都在这个公切面上。注意到空间中的三个球有两个公切面,因此三个圆锥的顶点必然都位于两个公切面的交线上。
证明 3 :想象你站在一个无穷大的平面上。有三个等大的球放在这个平面上,只不过由于有的球离你更近,有些球离你更远,因此这三个球看上去不一样大。每两个球确定了一个圆柱体,这三个横放在平面上的圆柱体将延伸到无穷远处,最终都消失在地平线处。看了这个“证明”后,你再看看本文最前面的图,是不是突然觉得这个定理很显然?