目前，我正在《新知客》杂志上主持一个趣题栏目。每月杂志发行后，我将在 Blog 上同步更新。点击 这里 可以查看往期题目。
推理
1. 高三 (17) 班有 50 个同学，他们的学号分别是 1, 2, 3, …, 50 。一次数学考试结束后，同学们都交完试卷离开了考场。数学老师小 A 清点试卷时发现，他手中只有 49 张卷子。究竟是谁没有交卷呢？正巧小 A 手边没有笔，他也不想把所有卷子按照学号重新排序。他希望不借助任何工具，仅仅通过依次查看每张卷子上写的学号，便能找出缺失的那个学号。和常人一样，小 A 的记忆力很有限，他没法记住之前到底看到过哪些学号；不过，作为一个数学老师，小 A 拥有无人匹敌的计算能力。他有办法找出没交卷的那位同学的学号吗？
2. 小 A 和小 B 玩游戏。从小 A 开始，两个人轮流从 1 到 9 当中选一个数（已经选过的数不能再选），约定谁先选到三个和为 15 的数，谁就获胜了。比方说，小 A 先选了 4 ，然后小 B 选 5 ，小 A 选 6 ，小 B 选 2 。为了阻止小 B 获胜，下一步小 A 就必须得选 8 （否则小 B 将靠 5 、 2 、 8 三个数获胜）。为了阻止小 A 获胜，小 B 选择了 1 （否则小 A 将靠 6 、 8 、 1 三个数获胜）。但是，这已经阻止不了小 A 的胜利了——小 A 可以选择 3 ，从而得到 4 、 8 、 3 三个加起来等于 15 的数。
在这个游戏中，小 A 有必胜策略吗？
计算
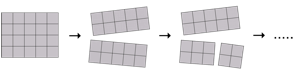
1. 有一块长方形的巧克力，它由 m×n 个小块组成。你想要把它们全部掰开。每一步，你只能拾起其中一块巧克力，沿着直线把它掰成两块。请证明，不管你用什么样的策略，把所有小块全部掰开所需要的步数都是相同的。
2. 把一副洗好的牌（共 52 张）背面朝上地摞成一摞，然后依次翻开每一张牌，直到翻出第一张 A 。下一张牌是黑桃 A 的可能性大还是黑桃 2 的可能性大？
填图：
1. 你能把一个等边三角形分成三个面积相等但形状各不相同的小三角形吗？
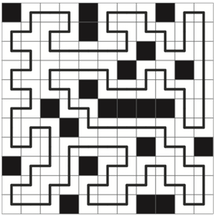
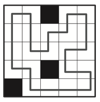
2. 像示例那样，在图中画出一条封闭的回路。这条路必须既无重复又无遗漏地经过每一个白色方格。
推理
1. 高三 (17) 班有 50 个同学，他们的学号分别是 1, 2, 3, …, 50 。一次数学考试结束后，同学们都交完试卷离开了考场。数学老师小 A 清点试卷时发现，他手中只有 49 张卷子。究竟是谁没有交卷呢？正巧小 A 手边没有笔，他也不想把所有卷子按照学号重新排序。他希望不借助任何工具，仅仅通过依次查看每张卷子上写的学号，便能找出缺失的那个学号。和常人一样，小 A 的记忆力很有限，他没法记住之前到底看到过哪些学号；不过，作为一个数学老师，小 A 拥有无人匹敌的计算能力。他有办法找出没交卷的那位同学的学号吗？
答案：首先算出 1 到 50 这 50 个数之和，它等于 1275 。然后从 1275 这个数开始，不断减去看到的学号，最后剩下的数就是缺失的那个学号。
2. 小 A 和小 B 玩游戏。从小 A 开始，两个人轮流从 1 到 9 当中选一个数（已经选过的数不能再选），约定谁先选到三个和为 15 的数，谁就获胜了。比方说，小 A 先选了 4 ，然后小 B 选 5 ，小 A 选 6 ，小 B 选 2 。为了阻止小 B 获胜，下一步小 A 就必须得选 8 （否则小 B 将靠 5 、 2 、 8 三个数获胜）。为了阻止小 A 获胜，小 B 选择了 1 （否则小 A 将靠 6 、 8 、 1 三个数获胜）。但是，这已经阻止不了小 A 的胜利了——小 A 可以选择 3 ，从而得到 4 、 8 、 3 三个加起来等于 15 的数。
在这个游戏中，小 A 有必胜策略吗？
答案： 1 到 9 中的三个数之和为 15 一共有 8 种情况：
1+5+9 1+6+8 2+4+9 2+5+8
2+6+7 3+4+8 3+5+7 4+5+6
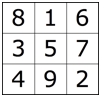
把 1 到 9 依照上图填进 3×3 的方阵中，方阵的每一行、每一列和两条对角线上的三个数之和都是 15 ，它们恰好涵盖了上述所有 8 种情况。因此，游戏的目标即是让自己选的数在方阵中成一条直线。也就是说，小 A 和小 B 在玩的其实是井字棋游戏！众所周知井字棋游戏是没有必胜策略的，因此在这个游戏中小 A 也是没有必胜策略的。
计算
1. 有一块长方形的巧克力，它由 m×n 个小块组成。你想要把它们全部掰开。每一步，你只能拾起其中一块巧克力，沿着直线把它掰成两块。请证明，不管你用什么样的策略，把所有小块全部掰开所需要的步数都是相同的。
答案：每掰一次后，巧克力的总块数都会加一。要想把一块巧克力掰成 m×n 小块，显然不管怎样都需要掰 m×n – 1 次。据说，这个简单得近乎荒唐的问题，有时竟能困扰数学教授们一整天的时间！
2. 把一副洗好的牌（共 52 张）背面朝上地摞成一摞，然后依次翻开每一张牌，直到翻出第一张 A 。下一张牌是黑桃 A 的可能性大还是黑桃 2 的可能性大？
答案：很多人可能会认为，下一张牌是黑桃 2 的可能性更大，因为刚才翻出的首张 A 可能就是黑桃 A 。其实这种直觉是错误的。令人吃惊的是，下一张牌是黑桃 A 的概率与下一张牌是黑桃 2 的概率一样大，它们都等于 1/52 。
为了说明这一点，我们不妨来看一种同样能实现绝对随机的另类洗牌方式：先把一副牌中的黑桃 A 抽出来，随机洗牌打乱剩下 51 张牌的顺序，然后把黑桃 A 插回这摞牌中（包括最顶端和最底端在内，共有 52 个可以插入的位置）。显然，黑桃 A 正好插到了这摞牌的首张 A 下面有 1/52 的可能性。同样的道理，首张 A 下面是黑桃 2 的概率也是 1/52 。事实上，任何一张牌都有可能出现在首张 A 的下面，它们出现的概率是相等的，都等于 1/52 。
填图：
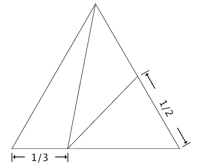
1. 你能把一个等边三角形分成三个面积相等但形状各不相同的小三角形吗？
答案：可以，如图。
2. 像示例那样，在图中画出一条封闭的回路。这条路必须既无重复又无遗漏地经过每一个白色方格。
答案：
我没看错哇。SF？
第一题直接想到位运算
大牛求解一题
A^2+B^3=C^4，A,B,C为正整数，求A,B,C的最小值？
发到qq邮箱吧 163的还得去网吧才能看了
3Q
计算 第二题 有问题
第一张A下面有牌的概率是 1
如果每张牌的概率是相等的是 1/52的话
那么第一张A出现在第一张A下面的概率就是1/52了。。。。
但这是0概率事件 因为没有两张相同的A
计算第二题 应当这样算
黑桃A在首A后
***A+黑桃A***A***A*** 计算时把 A+黑桃A算一张牌
一共有 51！种情况是黑桃A在首A后
而A+黑桃A 在 A+黑桃A***A***A 排在第一个概率是 1/3
总概率是 (51！/ 52!) * (1/3) = 1/156
黑桃2在首A后
***A+黑桃2***A***A***A*** 计算时把 A+黑桃2算一张牌
一共有51!种情况是黑桃2在首A后
而A+黑桃2 在 A+黑桃2***A***A***A*** 排在第一个概率是 1/4
总概率是 (51！/ 52!) * (1/4) = 1/208
由此可以看出实际上黑桃A出现概率更高
1/52的概率不满足模型的原因是
它是任意一张牌放在任意一张A后面的概率
与原题不符
后来的模型和原来的模型不一样
每次出概率题总是争议最大。哎~~~
不妨这样吧，总牌数改变总不会影响结论吧？想象只有5张牌，四张A一张2，问题变成高中填空题了。易知概率都是1/5，故原来那个也是一样。
呃~关于第一题，我以前用的方法是从25开始遇到奇数就加上，遇到偶数就减去，得到的数的绝对值就是少的那个。貌似减轻了不少计算量。
楼上的说法好像有问题,如果缺的学生是1号,跟缺的学生是3号,有什么分别?得出来的结不是一样吗?
九宫格+井字过三关那题在书上看过……
概率那一题虽然有点不相信,但是用C++运行出来的结果是:
黑桃A: .0196
黑桃2: .0188
好像真的没有太大差别
差点忘记中学学过的幻方
第一题，我想的是1275减去已交试卷学号之和，做加法总比做减法简单吧，最后再做一次减法
关于那个一笔画问题，有一个单机小游戏叫Hidato
巧克力那一題我想到用迴遞數列來解決。
A2 代表最基本的長方形，兩個小塊的，只需掰一次，所以 A2 = 1。
任何長方形必然是雙數的，所以任何有小塊數 m 的長方形：
Am = An + Am-n + 1。即把一個有 m 個小塊分成有 n 個小塊和 m-n 個小塊的兩塊巧克力的步數。
由於 n, m = 0 (mod 2)，所以 for any n，必然會成為 Am = xA2 + y 的形式。
计算第二题
“背面超上”应为“背面朝上”
回复：谢谢提醒，已改正
原来如此。。。
“井子棋”应为“井字棋”
回复：谢谢提醒，已改正
To 地基：
计算“***A+黑桃A***A***A*** ”的情况种数时还应该乘以首A可能是哪张A的可能性数(3)吧。
这样在计算黑桃2的时候，还应该乘以4。所以结果还是都是1/52。
一看就晕了！！嘎嘎
第一题用1+…+50 = 51 * 25 = 1275减去出现的学号，最后剩余的就数字就是没交的了。。。
晕，才看到答案。。无视楼上吧。。
对推理2答案有异议，题中没有说一定要选3个
A有必胜策略，比如A选依次选6（B会选9），5（B会选4），2，无论B下一个选什么，A的第四个都会获胜
同理，A可以依次选 （765） （856） （925），都可以保证选4个数就一定有15和
对推理2答案有异议，题中没有说一定要选3个
A有必胜策略，比如A选依次选6（B会选9），5（B会选4），2，无论B下一个选什么，A的第四个都会获胜
对推理2答案有异议
A有必胜策略，比如A选依次选6（B会选9），5（B会选4），2，无论B下一个选什么，A的第四个都会获胜
还有其他3组必胜策略 A选 765，856，925都可以保证取了第四个数后获胜
请无视我之前的评论
刚看到一定要3个数的和，这样的话6+9 7+8 不算赢，之前的评论错误
我懂了……第二题是和
“黑桃A/2的上一张牌是A”
作对比的
最后那个图可以推荐给fieldrunners做新地图哈哈
To hhdllhflower:
A^2+B^3=C^4，A,B,C为正整数，求A,B,C的最小值？
编了个程序跑了遍，A、B取100以内的话，有三组解：
{27,18,9}、{28,8,6}、{63,36,15}
这个地图蛮不错的。。。
第一题似乎是可以用xor来做的。。。
先算1xor2xor3xor4xor……xor50
在一个个的xor试卷号。。。。