趣题：面积为1的凸多边形总能放进一个面积为2的矩形里

证明：任意给定一个面积为 1 的凸多边形，我们总能把它放进一个面积为 2 的矩形里。
注意，这里“凸多边形”的条件是必需的——如果图形不是凸的，很容易想出反例来。

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

容易想到，对于面积为 1 的三角形来说，结论是成立的：

   

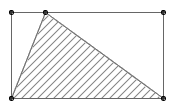
下面，让我们来考虑一般的情况。找出多边形中距离最远的两个点（以下图为例的话就是顶点 A 和 E ）。过这两个点作它们的连线的垂线（即下图中的两条水平线）。显然，多边形上的所有点都夹在这两条直线之间（否则会出现这些点到 A 或者 E 的距离大于 AE 的情况）。再在线段 AE 的两侧分别找出多边形上距离 AE 最远的点（即 C 、 G 两点），分别作 AE 的平行线。

   

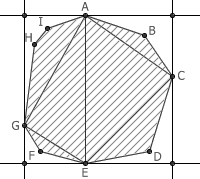
这四条直线形成的矩形完全包含了整个多边形，并且矩形的面积等于 △ACE 、 △AGE 的面积和的两倍，因而小于整个多边形面积的两倍。注意，在最后一步我们用到了凸多边形这一条件： △ACE 和 △AGE 一定在这个凸多边形的内部。

问题来源： http://www.cut-the-knot.org/Generalization/PolygonInRectangle.shtml

15 条评论

发表评论




Enter Captcha Here :