给你一张纸，要求你在上面画尽可能多的圆圈，使得所有圆圈都不相交。你最多能画多少个？
显然，你可以画无穷多个圆圈。事实上，你可以画不可数个圆圈——只需要画出一系列半径长均为无理数的同心圆即可。由于每两个无理数之间都夹有有理数，因此任意两个圆都没挨在一块儿。
给你一张纸，要求你在上面画尽可能多的叉，使得所有的叉都不相交。你最多能画多少个？
你可以画无穷多个不相交的叉。画法有很多，下图便是一种方案：
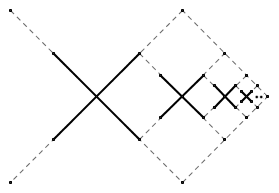
现在问题来了：你能在纸上画出不可数个叉吗？如果可以，请给出一种方案；如果不行，证明之。
答案是否定的。和画圆圈不同，你无法在纸上画不可数个叉。为了证明这一点，首先注意到，在纸上只能容下有限个单位大小的叉（从中心到四个端点距离都是 1 的叉）。这是因为，要想两个单位大小的叉不相交，两个叉的中心的间距必须要大于 1 才行，这就限制了单位大小的叉的总个数。
可是，纸上的叉可大可小，如何说明所有叉的个数是可数的呢？只需要把纸上的所有叉看作是“尺寸大于 1 的叉”、“尺寸大于 1/2 的叉”、“尺寸大于 1/4 的叉”、“尺寸大于 1/8 的叉”⋯⋯这可数个集合的并集就可以了。由于可数个有限集的并集一定是可数集，因此纸上最多只能有可数个叉。
题目来源：http://people.sc.fsu.edu/~jburkardt/fun/puzzles/tiny_writing_puzzle.html
哈哈！第一次沙发耶！
学习了~
板凳!!!
houhou,今天如此靠前
强！
学习了
……前排 夜自习时候困死了
画圈圈和画叉叉。。。噗。。。
做数学到深夜，看了这xxoo，又是完美的一天结束 了
嘿嘿,M大你是故意OOXX的吧
‘“尺寸大于 1 的叉”、“尺寸大于 1/2 的叉”、“尺寸大于 1/4 的叉”、“尺寸大于 1/8 的叉”⋯⋯这可数个集合的并集’——————这是可数个集合吗？ 应该是无穷集吧。古人云：一尺之锤，日取其半，永世不竭。
还请M牛详解
10F你没有理解“可数”的意思……
昨天晚上突然有一个想法，能否利用“这句话有七个字”这样自我指涉的句子，构建一个命题，与其逆否命题不同时成立或不成立。
“可数”是指countable infinite？
10F：你可能对可数集的定义不大清楚。我叙述一下有限集、无限集、可数集的定义。
如果集合A和集合B存在一个双射（A，B间的元素是一一对应的），称A和B是等价的。
如果有正整数n，使集合A与｛1，2，……，n｝等价，则A为有限集。否则称A为无限集。
如果A和N（正整数全体）等价，那么A成为可数集。换一句话说，A可数的充分必要条件是A中的全体元素可以排列成a1,a2,…,an,…的形状。（所以说，可数集是无限集，但是无限集不一定是可数集，可能是不可数集。）
*****************************************************
很巧啊。今天我的泛函分析的课上，证明了一个集合是可数时。老师也用了证明纸上有可数个叉叉的方法。
多谢楼上同学的解释 :-)
只需要把纸上的所有叉看作是“尺寸大于 1 的叉”、“尺寸大于 1/2 的叉”、“尺寸大于 1/4 的叉”、“尺寸大于 1/8 的叉”⋯⋯这可数个集合的并集就可以了。由于可数个有限集的并集一定是可数集，因此纸上最多只能有可数个叉。
这些可数集合的个数貌似是不可数的吧. 不可数个可数集合的并集也是可数的?
@ idy:
明白了. 证的是X的个数是可数的.
= =~话说 您更新博文的频率还是很高的
一直在看呢~
我见过话8字的= =,同一个问题
我来证一个：对每一个叉叉，在它中心点左边附近（比如边长的0.01倍到0.02倍之间之内）取一个有理点，右边也取一个有理点。显然不相交的叉叉不可能有相同的点对。因此叉叉的个数不多于有理点对的个数，是可数的。
可数个有限集的并集一定是可数集
原来如此。
可是我可以在每个圆圈里画一个叉叉啊？
可是可以在每个圈圈中画一个叉叉啊？
可是圆环套圆环啊
我可不可以在最大和第二大圆之间的空隙里都画一个X呢？再加上最小的O里一个X，那X和O的数不就相等了，是不是就不可数了呢？
我可不可以在最大和第二大圆之间的空隙里都画一个X呢？再加上最小的O里一个X，那X和O的数不就相等了，是不是就不可数了呢？
回复的时候碰到500错误了…
这个问题挺有意思的，我想知道M同学是一个人呢，还是一个团体呢，对他不太了解
楼层: 10楼 | 2010-10-26 11:38 | hillwhite 说：
‘“尺寸大于 1 的叉”、“尺寸大于 1/2 的叉”、“尺寸大于 1/4 的叉”、“尺寸大于 1/8 的叉”⋯⋯这可数个集合的并集’——————这是可数个集合吗？ 应该是无穷集吧。古人云：一尺之锤，日取其半，永世不竭。
还请M牛详解
求解
楼层: 24楼 | 2010-10-28 18:29 | sixdegree 说：
可是可以在每个圈圈中画一个叉叉啊？
事实上，在不可数个oo中，只有可数个oo间可以画xx
21楼的证发很强势。
同顶21楼
回26楼，参看30楼的解答。
事实上，在不可数个oo中，只有可数个oo间可以画xx
——
这个怎么证明呢？
感谢15楼elly66补充！
俩个都可以连接在一起咯
15楼解释很详细，谢谢