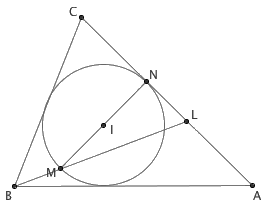
动脑时间咯!搞搞几何题,脑子不生锈。作出任意三角形 ABC 的内切圆 ⊙I ,它与 AC 相切于点 N 。过 N 作 AC 的垂线,与 ⊙I 的另一个交点记作 M (因此 MN 就是这个圆的一条直径)。连接并延长 BM ,与 AC 交于点 L 。求证: CN=AL 。
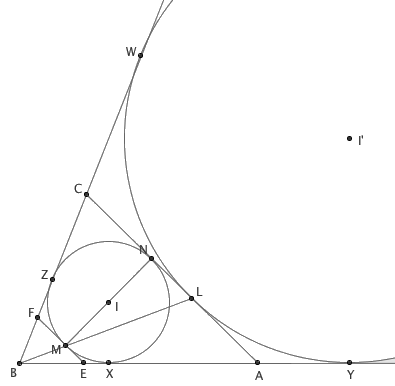
下面这个证明方法很妙:过 M 点作 ⊙I 的切线,与 AB 、 BC 分别交于点 E 、 F 。因此, EF 与 AC 平行。以 B 点为中心,把 △BEF 放大到 △BAC ,则 M 点就会和 L 点重合,而 ⊙I (作为 △BEF 的旁切圆)则会变成 △BAC 的旁切圆 ⊙I’ 。
下面我们要用到与切线长相关的两个定理:
(1) 两圆的两条外公切线等长
(2) 圆外一点到圆的两条切线等长
由 (1) 可知 XY = ZW ,即 AX + AY = CZ + CW 。由 (2) 可知 AX 、 AY 、 CZ 、 CW 分别等于 AN 、 AL 、 CN 、 CL 。于是有 AN + AL = CN + CL 。等式两边都减去 NL 一段,有 2 * AL = 2 * CN ,结论就证到了。
问题来源:http://www.cut-the-knot.org/Curriculum/Geometry/PerpIndiameter.shtml