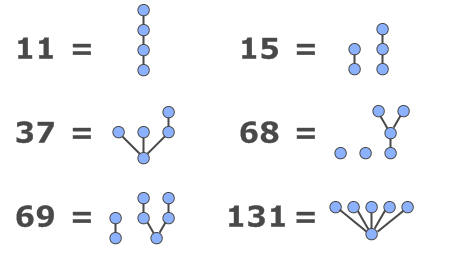
你能找出规律吗？明天晚上公布问题答案，并探讨一些延伸话题。
Update: 抱歉昨晚有些突发情况，没能更新。
这个问题来自于 这里 。没错，图中的规律就是：每棵树代表一个质数，一个森林（若干个树放一块儿）就表示这些质数的乘积；如果一个森林表示的是 n ，在这个森林下方添加一个公共根，就构成了新的质数——第 n 个质数。例如， 69 就等于 3 乘以 23 ，它们分别是第 2 个质数和第 3×3 个质数。 131 这个例子更能说明问题，因为它就是第 32 个质数。
这个东西牛就牛在，它建立了一个自然数到森林的一一对应关系（从而也就建立了自然数到有根树的一一对应关系，因为我们可以用添加超级根的方法把森林都视作树）。这种为有根树编号的方法叫做 Matula-Goebel 编号法，参见数列 A127301 。
注意到质因数分解在构造一一对应关系中的妙用。正是因为有唯一分解定理，数的表示方法才是唯一的。于是乎，图论和数论巧妙地结合在了一起，实在令人拍案叫绝。
SF!
….!
没头绪呀。。
牛！ 但找不到规律～～～
请问能否多给几个?太难了
貌似找到点规律了 不过又有点不一样的地方
我想问一下matrix67
这个规律能否表示1？难道什么都不写就是1？
69的表述方法是否正确？
唉，先上课去了。。。
乘法
15=3*5
68=2*2*17
69=3*23
感觉楼上的有道理，和质因数分解表示应该有关，但是质数的表示方法还没找到规律，特别是分叉，貌似和找烃的同分异构体有点像
ps：偶是学化学的。。。
o 2 第1个质数
o -o 3 第2个质数
o -o-o 5 第3个质数
o -o
| -o 7 第4个质数
o -o-o-o 11 第5个质数
o -o-o
|-o 17 第7个质数
o -o-o
| -o-o 23 第9个质数
o -o
| -o
| -o-o 37 第12个质数
o -o
| -o
| -o
| -o
| -o 131 第32个质数
看懂了么
质数位是去掉树根后的表示
举例
o-o-o-o-o 31
是第11个质数
o-o-o-o 11
是第5个质数
o-o-o 5
是第3个质数
o-o 3
是第2个质数
o 2
找的累死了，TAT
举例
o-o
|-o
代表第4个质素7
去掉根后
是 o o
就是2*2=4
非质数分解为多棵子树，每个子树表示这个数的一个质因数；
1是什么都没有。
其他的质数——不妨设为第i个质数，那么这个质数的树去掉根以后剩下的一个森林就是i
非质数分解为多棵子树，每个子树表示这个数的一个质因数；
1是什么都没有。
其他的质数——不妨设为第i个质数，那么这个质数的树去掉根以后剩下的一个森林就是i.
楼上花了多少时间哈
我花了一个半小时TAT
懂了
楼上各位牛，我是一点也看不出来。
同意10楼的，但是这样表示有什么用处呢？
干嘛要纠结它的用处呢？
质数和乘法 突破口是 11 37 和131是一棵树 其他的是森林
God help me, I put aside a whole afnrteoon to figure this out.
10楼的是牛人啊！
期待明天。
挺有趣的，任意一个质数都能表示成一棵树，有很多大质数因子的合数就能成为一片森林。
我想语言描述的规则应该是这样的：对某一个合数m，假设它能分解为三个质因数xyz，那m的表示就是xyz并排在一起所组成。而对于比如x这个质数的表示法，假设x为第i号质数，i能分解为pq的乘积，将pq的树枝表示法并排在一起，下面添加一个节点，再连接起来。如果i本身即为质数，则画出i的表示法，下面添加一个节点即可。如上面有人说提到，1必须定义为空。
这样的描述似乎太复杂，说不定背后有更本质更简单的规则。
囧。。硬是要凑片森林出来咩。。
树的个数表示质因数的个数。一棵树表示一个质数。树的深度表示进位，叶子节点表示2，即第一个质数。从图中最上面一级开始，每往上一级进一位，进位的方法是以本级表示的质数（记为n）作为序号，算出第n个质数即为下一级所表示的质数。如果在同级有其他节点，则所有同级节点所表示的质数相乘，参与下一级运算。最终计算到根节点。
我想问下，是否考虑过指数的表示法。。否则类似65536之类的数表示起来比较辛苦。。
还有就是，0怎么表示。。
等明天一个简洁的表述（结论）。多谢LS各位朋友指导！
67，这图用什么画的，看起来挺舒服的
每个起点初始值为第一个质数2,如上一个点的值为n，则下一个点的值为第n个质数；并行的点要做乘法运算
有点意思，大学的时候有学过
从有根森林同构类的集合到正整数集的一一对应a->f(a)，满足：
(空)->1
(a,b的并)->f(a)*f(b)
(用一个新的根节点连结到a的所有根节点)->第f(a)个质数
有意思，呵呵
写了个Python代码：
prims = [2]+[d for d in xrange(3, 10000, 2) if 2 ** (d -1) %d == 1]
def get_fac(n):
li = []
while n not in prims:
for x in prims:
if n % x == 0:
li.append(x)
break
n /= li[-1]
li.append(n)
return li
def get_tree(n):
if n == 1: return []
if n in prims:
return [get_tree(prims.index(n) + 1)]
return [get_tree(x)[0] for x in get_fac(n)]
x = lambda n: “, “.join(map(str, get_tree(n)))
print x(11)
print x(15)
print x(37)
print x(68)
print x(69)
print x(131)
？？？
一个有限长度的数列，可以有无限个通项公式，本题也是。
与找通项公式的方法类似，对于这个题目寻找通项公式的方法可以是这样的：
1) 设计一种编码方法，构造两个矩阵以表达这颗树
比如这样：
a) 观察发现节点数目最多5列，最多4行，于是构造一个4X5的矩阵M1，如果对应位置有节点，则设其数值为 X，如果没有则设其数值为 Y，其中X 和 Y任意选择，只要不相等即可。
b) 观察发现节点之间连接关系之后上下之分，也就是说总共有10种可能的连接方向。可以选择10个不同的数值代表不同的连接方式，再加上不相连这一种情况，对于每一个节点，可以由一个11维的向量 Z 表示连接关系，然后选择一个函数 f，令f(Z)作为某种连接方式的唯一编码。于是将每一个节点的连接方式的编码填充进去，可以再构造出一个 5X4 的矩阵 M2。
2) 选择一个函数 g，只要使得 g(M1, M2) 数值为主贴中给定的数值即可
具体来说：
对于a)，可以令 X=1, Y=0
对于b),f(Z)的结果可以是一个11个位的整数，每一位是1则代表相连，0则代表不相连
对于2)，可以选择将 M1和M2中的元素依次填充到一个40维的向量a中，然后再寻找一个40维的向量x，令它们的点积为表示的数。也就是化简为一个方程组：A x = b
由于主贴给出 6 个用例，因此 A 是一个 6X40 的系数矩阵， x 是一个40 维的未知向量，而 b 是{11, 15, 37, 68, 69, 131}
非质数分解为多棵子树，每个子树表示这个数的一个质因数；
1是什么都没有。
其他的质数——不妨设为第i个质数，那么这个质数的树去掉根以后剩下的一个森林就是i.
34楼代码第一行就错了，费马小定理的逆命题是错误的，比如341就是一个反例。
然后后面的东西没有缩进看不懂啊……
质数？看完题目第一反应是这个
39L: 你说得对，那我改成另外的函数吧。缩进这个………………真不好解决，我就在前面加点东西吧~~~
|prims = reduce(lambda s, x: s + ([x] if all([x %i for i in s]) else []),
| range(2,10000), [])
|
|def get_fac(n):
| li = []
| while n not in prims:
| for x in prims:
| if n % x == 0:
| li.append(x)
| break
| n /= li[-1]
| li.append(n)
| return li
|
|def get_tree(n):
| if n == 1: return []
| if n in prims:
| return [get_tree(prims.index(n) + 1)]
| return [get_tree(x)[0] for x in get_fac(n)]
|
|x = lambda n: “, “.join(map(str, get_tree(n)))
|
|print x(11)
|print x(15)
|print x(37)
|print x(68)
|print x(69)
|print x(131)
|
|
我晕…………这样都不行…………
那只有这样了…………
|prims = reduce(lambda s, x: s + ([x] if all([x %i for i in s]) else []),
|……………range(2,10000), [])
|
|def get_fac(n):
|….li = []
|….while n not in prims:
|……..for x in prims:
|…………if n % x == 0:
|…………….li.append(x)
|…………….break
|……..n /= li[-1]
|….li.append(n)
|….return li
|
|def get_tree(n):
|….if n == 1: return []
|….if n in prims:
|……..return [get_tree(prims.index(n) + 1)]
|….return [get_tree(x)[0] for x in get_fac(n)]
|
|x = lambda n: “, “.join(map(str, get_tree(n)))
|
|print x(11)
|print x(15)
|print x(37)
|print x(68)
|print x(69)
|print x(131)
|
|
美，任何一个自然数都有唯一的质因子分解，任一一个质数都和自然数（质数的顺位）一一对应。
我只是想知道“1”是怎么表示的啊？
它只能表示2以上的数吗？
有啥应用啊？
11=* *
*
可以吗
相当有创造性，相当有建设性。
可以很容易地用一个递归程序实现。
哇，最近正好在想相关的问题。
二叉树或者n-叉有根数到自然数的bijection是非常容易构造的
有根树到自然数集的bijection我想了好久也没想出来，今天居然在这里看到了，真巧妙。
这样，有根树就可以和二叉树建立bijection，因为用自然数集中转一下就好了。那么，如果不通过这样的中转，有没有什么直接而又简单的方法直接建立这个映射呢？
挺有意思的
11为什么是4个，不是5个么？
50 楼:
因为 5 是第 3 个质数
话说M67对数学这么有爱，没来学数学真是可惜…
很精辟！
为什么11是4个点? 11不是第5个质数吗? 2,3,5,7,11第5个啊
因为第 4 个质数 7 是用 2 * 2 也就是森林表示把
因为第 4 个质数 7 是用 2 * 2 也就是森林表示吧
分解的一一对应
好耍!据说,中国某地发现神秘麦田怪圈,现状为树形.
经m67破解之后,惊人的发现竟然是
2012.12.25
我怎么觉得11应该是用五个连线的点点表示？它是第五个质数啊
真的很好玩啊，看了好久才看懂，呵呵
那个什么，
RE：为什么11是4个点？
4个点是在3个点下面加1个点，意为第“3个点表示的数”个质数
一个点是第一个质数2,两个点是第2个质数3,三个点是第3个质数5，四个点是第5个质数11。。。
于是发现这样的设置好神奇，有些“正好”的因素呢。
然后貌似会有一组质数，只能用一串点来表示。。第11个质数31（5个点），第31个质数XXX（6个点）。不知算不算一种“特殊情况”？
为什么我这么罗嗦。！
很有意思的问题哦，我当时第一眼就看出11，37，131是素数，接下来花了20分钟时间就破解了。
有谁能够写个mathematica程序，给出数字，画出对应的森林呢？
这个数论—图论的链接确实很巧妙 不过 有一点想请教一下博主:请问“因为我们可以用添加超级根的方法把森林都视作树”请问这个是什么意思啊？如何添加这个“超级根”呢？谢谢您！^_^
呵呵 我想出来了！
很有创造力的想法，真的不错。
想通后，觉得，这一片森林好可爱啊~
因为第 4 个质数 7 是用 2 * 2 也就是森林表示吧
分解的一一对应
这是不是和[序数]数学有关系？有没有相关的keyword？
春风尔来为阿谁，蝴蝶忽然满芳草。