切片引理和两个意想不到的应用

    考考你的立体几何直觉：用一系列间距相等的平行平面把一个球体切成厚度相同的薄片，这些薄片的侧面积都相等吗？

  

    是的。用平行平面把球体截成一个个切片，如果切片的厚度都相同，那么它们的侧面积也都相同，不管这些切片位于球体的什么位置。也就是说，切片的侧面积是与切片的厚度成正比的。推导这个惊人的结论非常适合用作定积分计算旋转体侧面积的练习题。圆的表达式是 √1 – x^2 ，套用公式 ∫(a..b) 2π·f(x)·√1 + f'(x)^2 dx 即可发现，整个积分被化简为 ∫(a..b) 2π dx ，因此薄片侧面积就是 2π(b-a) 。换句话说，半径为 1 的球里，一个切片的侧面积总等于 2π 乘以切片的厚度，两个切片的侧面积相等当且仅当它们的厚度相等。我查了半天，似乎这个经典结论并没有什么特别的名字，不妨就把它叫做“切片引理”吧。

 
  

    有趣的是，这个定理在二维情形是不成立的。比方说，取半径 OA 的中点 M ，过 O 和 M 分别作半径的垂线。由于 OM 是 OB 的一半，可知 ∠AOB=60° ， ∠BOC=30° ，弧 AB 和弧 BC 明显不相等。

 
    最近，我看到了两个非常有趣的问题，它们与上述引理非常奇妙地联系在了一起。其中一个问题是：用圆规在平面上和在球面上各画一个圆，哪个圆大一些？考虑一些特殊情况，我们会非常惊奇地看到，两个圆竟然是一样大的！比方说，设球的半径为 1 ，取圆规两脚的距离为 r＝√2 ，则在平面上圆规将画出一个半径为 √2 的圆，面积为 2π ；圆规将在球上画出赤道线，这个“圆”的面积就是一个球的表面积的一半，也是 2π 。

     

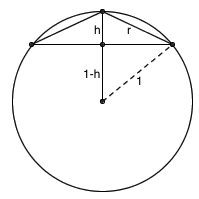
    在一般情况下，这也是成立的。若圆规两脚间距为 r ，在半径为 1 的球上画圆，则它圈出来的面积就是一个高为 h 的切片侧面积，其中 h 满足 r^2 – h^2 = 1 – (1-h)^2 ，可解出 h = r^2/2 。根据前面的结论，切片的侧面积就是 r^2/2 的 2π 倍，即 πr^2 。

 
    另一个有趣的问题来自于一个经典的竞赛题目：用有限多个长度无限、宽度有限的“带状区域”能否覆盖整个平面？答案是否定的。我们下面说明，给你一些宽度和为 1 的纸带，你甚至不能覆盖一个半径为 1 的圆。因为，一个宽度为 w 的纸带与单位圆的公共面积不可能超过 2w ，因此所有纸带与圆的公共面积之和不可能超过 2 ；但圆面积为 π ，这个值远远比 2 大，结论也就证到了。
    上述推理过程告诉我们，要想覆盖一个单位圆，需要一组宽度和至少为 π/2 的纸带，但很明显 π/2 这个下界还是太松了。事实上，为了覆盖一个单位圆，纸带的宽度和为 2 是充分且必需的。充分性很显然——把纸带从上到下一张一张平行地摆放就可以了。因此，接下来我们就着重研究它的必要性。如何说明一组覆盖单位圆的纸带，它们的宽度和至少为 2 呢？下面我们给出一个巨牛无比的诡异证明，它是我见到的又一个把平面图形扩展到空间之后立刻秒杀的问题。

     

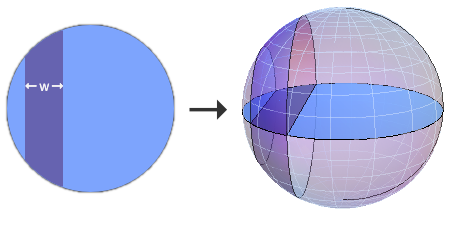
    把这个单位圆想象成是一个单位球中的过圆心的截面。我们把圆上的每一条纸带都投影到球的表面上。假如这个纸带的宽度是 w ，不管纸带在圆上的什么位置，它在球上的投影面积总是 2πw 。一组覆盖了整个单位圆的纸带，其投影必然也覆盖了整个球面；然而球面的总面积是 4π ，因此所有 w 之和至少为 2 才行。

37 条评论

发表评论




Enter Captcha Here :