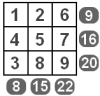从本月起，我开始在《新知客》杂志上主持一个趣题栏目。每月杂志发行后，我将在 Blog 上同步更新。
推理：
1. 老王熬夜工作到凌晨 2 点多时，实在不行了，倒在床上就开始呼呼大睡。睡觉前他看了一下闹钟，发现了一件有趣的事情——时钟上的时针和分针正好重合在了一起。早晨 8 点多时，老王被闹钟闹醒。他看了一下闹钟，又发现了一件有意思的事——此时时钟上的时针和分针正好指向完全相反的方向。老王究竟睡了多久呢？不足 6 个小时， 6 个多小时，还是正好 6 个小时？
2. 小 A 、小 B 和小 C 竞选推理协会的会长，有 99 个人参与了投票（当然，三位候选人是不能参与投票的）。唱票后，三位候选人惊奇地发现，每个人各得了 33 票。为了分出胜负，小 A 提议，每个投票人都选出自己心目中的“第二人选”。巧合的是，第二轮投票之后，三个人又是各得 33 票。接下来该怎么办呢？小 A 注意到了投票的人数是奇数，于是想到了一个一定能决出胜负的投票方案：所有投票人先在小 B 和小 C 当中进行投票，获胜者再和小 A 进行 PK 。这时，小 B 突然站出来反对：这种方案是不公平的，这对小 A 明显更有利一些。小 B 的说法对吗？
计算：
1. 周长相等的正三角形和正六边形，面积之比是多少？
2. 平面上有 n 个红点和 n 个蓝点，你需要把它们一红一蓝地配成 n 对，并用线段把每一对点连接起来。证明，总存在一种配对方案，使得所有连线都不交叉。
填图：
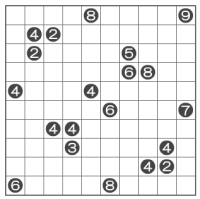
1. 把图中的棋盘划分为一个一个的矩形，使得每个矩形中恰好包含一个数字，而这个数字恰好等于这个矩形中的小方格数。
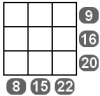
2. 把 1 到 9 这九个数字填入方格中，使得每行三个数之和等于这一行右边的数，每列三个数之和等于这一列下方的数。
推理：
1. 老王熬夜工作到凌晨 2 点多时，实在不行了，倒在床上就开始呼呼大睡。睡觉前他看了一下闹钟，发现了一件有趣的事情——时钟上的时针和分针正好重合在了一起。早晨 8 点多时，老王被闹钟闹醒。他看了一下闹钟，又发现了一件有意思的事——此时时钟上的时针和分针正好指向完全相反的方向。老王究竟睡了多久呢？不足 6 个小时， 6 个多小时，还是正好 6 个小时？
答案：正好 6 个小时。在这 6 个小时里，时针转了一个半圈，分针转了 6 个整圈，因此两针正好指向了相反的方向。
2. 小 A 、小 B 和小 C 竞选推理协会的会长，有 99 个人参与了投票（当然，三位候选人是不能参与投票的）。唱票后，三位候选人惊奇地发现，每个人各得了 33 票。为了分出胜负，小 A 提议，每个投票人都选出自己心目中的“第二人选”。巧合的是，第二轮投票之后，三个人又是各得 33 票。接下来该怎么办呢？小 A 注意到了投票的人数是奇数，于是想到了一个一定能决出胜负的投票方案：所有投票人先在小 B 和小 C 当中进行投票，获胜者再和小 A 进行 PK 。这时，小 B 突然站出来反对：这种方案是不公平的，这对小 A 明显更有利一些。小 B 的说法对吗？
答案：小 B 是对的——在新的方案下，小 A 将必胜！为了说明这一点，我们把投票人的偏好分成六类：
(1) A > B > C
(2) A > C > B
(3) B > A > C
(4) B > C > A
(5) C > A > B
(6) C > B > A
由于第一轮投票是平局，因此 (1) (2) 的总人数、 (3) (4) 的总人数、 (5) (6) 的总人数各占 1/3 。也就是说，如果要在小 B 和小 C 之间进行 PK 的话，就全看 (1) 和 (2) 的人数谁多谁少了。不妨假设 (1) 的人数比 (2) 多（这样的话小 B 将在 PK 中获胜，并与小 A 对决），那么 (4) 的人数就一定比 (3) 多，否则 (2) (4) 的总人数将不足 1/3 ，小 C 不可能在第二轮投票中与小 A 和小 B 战平。类似地， (5) 的人数就一定比 (6) 多，否则 (3) (5) 的总人数将不足 1/3 ，小 A 不可能在第二轮投票中与小 B 、小 C 战平。既然 (5) 的人数比 (6) 多，那么在小 A 和小 B 之间进行最后的角逐，小 A 一定会获胜。
对于 (2) 的人数比 (1) 多的情况，类似的分析可以推出同样的结果来。
计算：
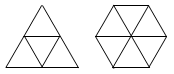
1. 周长相等的正三角形和正六边形，面积之比是多少？
答案：把它们都剖分成完全相同的小正三角形，很快就能看出它们的面积比是 2:3 。
2. 平面上有 n 个红点和 n 个蓝点，你需要把它们一红一蓝地配成 n 对，并用线段把每一对点连接起来。证明，总存在一种配对方案，使得所有连线都不交叉。
答案：考虑所有可能的配对方案，选择所有连线的长度总和最小的那一种方案。下面我们证明，这种方案是满足要求的。假如在这种方案中有某四个点 A 、 B 、 C 、 D ，其中红点 A 和蓝点 B 相连，红点 C 和蓝点 D 相连，两条连线交于点 O 。那么，把它们改成 A 与 D 相连， B 与 C 相连，则由三角形两边之和大于第三边， AB + CD = (AO + DO) + (BO + CO) > AD + BC，说明连线的总长度变得更短了，由此产生矛盾。
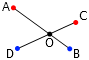
（图已更正）
填图：
1. 把图中的棋盘划分为一个一个的矩形，使得每个矩形中恰好包含一个数字，而这个数字恰好等于这个矩形中的小方格数。
答案：
2. 把 1 到 9 这九个数字填入方格中，使得每行三个数之和等于这一行右边的数，每列三个数之和等于这一列下方的数。
答案：
沙发~
假设
“从本月起，我开始在《新知客》杂志上主持一个趣题栏目。”
膜拜。。
红点 C 和蓝点 D 相连，图配错了。。
不过题目貌似都很简单。。
借地方求问，想DIY生日礼物送给geekBF，求这个blog上的geek们帮忙出主意，除了分形三角形手机链……谢谢-_-b
怎么让我想起了马丁加德纳
这个杂志的销量绝对会因为你的第一句话大增。。
我就喜欢玩推理题…
真的很有趣nia~
这就是您很久之前说的给杂志投稿么…
这也太慢了… – -|||
开始买杂志…
填图第一题叫作shikaku，是日本人发明的谜题好像。
M67牛玩数独吗？欢迎来百度数独吧逛逛。
jcvb
你好，我订阅你的博客很长时间了，非常喜欢。我也写过一些谜题相关的文章，不仅有谜题，还融合了故事性，而且是原创（谜题是部分改编，部分原创，故事情结是完全原创）。
有兴趣可以给我发邮件，我会把作品发给你。如果觉得还行，你也可以把我推荐到新知客，嘿嘿~
回地基：
哪种Geek？
如果是数学Geek，买件纯白体恤正面印上纯黑色e^(iπ)+1=0，记住字母要斜体，指数是上标型。整件体恤上只能有一个公式。背面印上下图中中间那个。
[IMG]http://www.i3721.com/cz/tbjak/bnj/hsdb8njsx/200605/%D3%C3%B9%B4%B9%C9%B6%A8%C0%ED%D3%EB%CD%E2%D0%C7%C8%CB%C1%AA%CF%B5.files/image002.jpg[/IMG]
啊啊啊，受不了了，我自己都好想要……做两件给我一件吧。 -_-|||
回LS：
谢谢回复T_T
其实是工科geek，然后，链接打不开呀打不开。。
不过还是谢啦：）
继续等回复，这个BO上的geek们你们在哪里啊在哪里……
红点蓝点那题不是巨人与鬼那题吗
连线那题不是很简单吗，只要不出现闭曲线是不可能把平面分成两部分的，所以每次连接两个点都能成功。
很喜欢3人投票的题目。
我在想，如果照那样的提议投票，第2轮的成绩，是不是一定是A得到2/3（66）票，另一个得到1/3（33）的票呢？
空会想不会证明！
周长相等的正三角形和正六边形，面积之比是多少
我小学升初中的考试题。。。记得当时算对了然后写反了
我在这里看到这个杂志后，第一时间去Google了一下，结果，我好想买
哇哇哇哇~~~~~我有一直在买《新知客》诶！ 。。。只是暑假了，停了一个月。。。 好！开学了再去买。。还是订阅好了，实惠些。
计算第二题可以用归纳法证明吗.
选举这一题，我的第一反应是，设想三个候选人是剪刀、石子、布的相克关系，这样淘汰任何一人，都是对剩下的一对造成不公平。
这样立刻发现答案的证明中用到了隐含的假设，选举人对候选人的偏好满足传递关系，而这是题中没有交代的。
计算第二题好像有问题。
假设有四个点，在同一条直线上，其中两个红的在左边，两个蓝的在右边。这种情况无法实现不相交。
有时候的数学题目就是这样的
膜拜
很有趣的图案。。。
投票人都拿了枪，BC冲出去了，有人向他们开枪，回来了一个，A和回来的这个一起出去，又被干掉了一个，A只出去了一次，所以有优势。
面积比那个，不需要画图。直接设周长为3
1.毫无疑问三角形的面积是0.5(简单点想，旋转180看成漏斗那样，下沉就是个菱形了，但是面积扩大了1倍)
2.同样的正6边形就是3菱形，0.5*0.5*3（0.5是3/6正六边形的边长）
就是 0.5：0.75 ，我写的比较啰嗦，但人脑基本上是秒证。
周长换成x就是这样的：
x/3 * x/3 /2 （3是边的数量，/2 是因为扩大了还回去）
x/6 * x/6 /3 （6是边的数量，/3 是看作三个菱形构的）