前几天，我看到了这样一个问题：如何用火柴棒准确地搭出一个正方形？注意，由于没有任何工具可以让两根火柴棒拼成一个 90° 角，因此用四根火柴棒随意摆出一个四边形，最多也只能是个菱形。要想拼出一个正方形，我们还得想些奇招来。

      

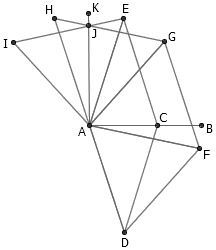
    一个经典的做法如上图所示。先摆出线段 AB ，下面我们将要确定线段 AK 的位置，使得两条线段成 90° 角。在 AB 上随意找一个点 C ，以 AC 为底搭出两个腰为 1 的等腰三角形 DAC 和 EAC 。容易看出， D 、 E 是关于 AB 对称的两个点。搭建一系列等边三角形 △ADF 、 △AFG 、 △AGH ，确定出 D 关于 A 点的对称点 H 。这样， H 、 E 两点就关于 AK 轴对称了。再搭一个等边三角形 AIE ，则 I 、 G 两点也关于 AK 对称。因此， HG 和 IE 的交点 J 就在 AK 上，自然 AK 的位置也就确定出来了。重复执行以上操作，我们便能完成以 AB 为边的整个正方形。

    受此启发，我们自然而然地想到了这样一个问题：火柴棒的几何作图能力到底有多强？我们能仅凭借火柴棒找出三角形的外心吗？我们能仅凭借火柴棒搭出一个正五边形吗？ 1939 年， T. R. Dawson 在一篇论文中证明了一个惊人的结论：火柴棒作图与尺规作图的能力完全一样！换句话说，用尺规作图能够确定的点，用火柴棒作图也能确定；而尺规作图办不到的事，火柴棒作图也没法办到。也就是说，火柴棒作图完全等价于尺规作图！

    为了证明这一结论，我们首先得给火柴棒作图下一个定义。我们约定，用火柴棒作图时只允许以下四种基本操作，它们就是火柴棒几何中的“公理”：

1. 给定一点 A ，可以作一条通过 A 的单位长线段，或者以 A 为端点的单位长线段
2. 给定距离不超过单位长的两点 A 、 B ，可以作一条通过 A 、 B 的单位长线段，或者以 A 为端点过 B 的单位长线段
3. 给定距离不超过单位长的两点 A 、 B ，可以以 AB 为底作一个腰为单位长的等腰三角形 ABC 。
4. 给定距离不超过单位长的点 A 和直线 l ，可以作一条以 A 为端点，另一端点在 l 上的单位长线段

    有了这些基本操作，我们便可以一步一步搭出火柴棒的几何世界了。

 
    延长一条线段

      

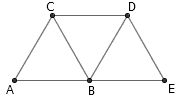
    如上图，搭出一系列等边三角形，我们便能实现线段的延长。注意到线段 CD 与 AB 平行且相距 √3/2 个单位，因此我们还得到了一个非常有用的工具：将给定线段平移 √3/2 个单位。

 
    找出长度小于单位长的线段的中点

      

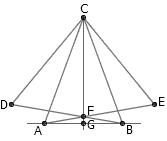
    如图， AB 为已知线段。先作等腰三角形 ABC ；再作等边三角形 BDC 和 AEC 。 BD 和 AE 的交点 F 就在等腰三角形的中线上。 CF 的延长线与 AB 的交点就是我们所求的点 G 。
    由于 CG 还平分了 ∠ACB 和 ∠DCE ，因此我们相当于有了一个平分不超过 120° 且不等于 60° 的角的办法。另外，由于 CG 还是 AB 的垂线，因此我们又有了过点 C 向已知线段作垂线的方法——先利用公理 4 摆出线段 CA 和 CB ，再找出 AB 的中点。即使 C 点离已知线段很远，垂线照样作得出，因为我们可以将已知线段不断平移 √3/2 个单位，让它与 C 的距离足够近。不过，这里还是有一种特殊的情况：若 C 与已知线段的距离恰好是 √3/2 的整倍数，这么做就不行了。

 
    找出长度等于单位长的线段的中点

      

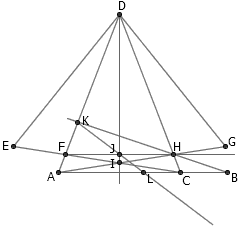
    假如 AB 是一条长度恰为单位长的已知线段。首先在 AB 上任取一点 C ，然后作等腰三角形 ADC 。作等边三角形 CED ，与 AD 交于 F ；作等边三角形 AGD ，与 CD 交于 H ； CE 和 AG 交于点 I 。那么， DI 与 FH 的交点 J 就是 FH 的中点。 BH 与 AD 交于点 K ， KJ 与 AB 交于点 L ，于是我们就成功地把 FH 的中点转移到了 AB 的中点。
    这个构造弥补了我们之前留下的空缺。现在，我们不但能平分恰为 60° 的角，也能引出距离恰为 √3/2 的整倍数的垂线了。

 
    过已知线段外的一点，作已知线段的平行线

      

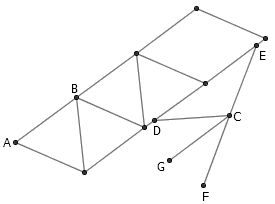
    不断平移已知线段 AB ，直到它离点 C 足够近。以 C 为端点，利用公理 4 引单位长线段 CD 、 CE 。反向延长 CE 到 F ，则 ∠DCF 的平分线 CG 就与 AB 平行。

 
    找出距离大于单位长的两点的中点

      

    已知很远的两点 A 、 B 。向任意方向作单位长线段 AC ，过 B 作它的平行线段 BD 。利用一系列等边三角形，构造逐渐向中间靠拢的中心对称图形，直到出现距离不超过单位长的对称点 E 、 F 。 EF 的中点也就是 AB 的中点。
    既然我们能找到任意线段的中点，平分大于 120° 的角也就不成问题了。

 
    好了，准备工作基本结束，下面我们就来说明火柴棒作图与尺规作图的等价性。注意到，火柴棒作图的四项基本操作都能用尺规作图实现，因此火柴棒作图是尺规作图的子集。为了说明尺规作图同时也是火柴棒作图的子集，我们只需要用火柴棒实现尺规作图的三个基本操作：作出过两点的直线、作出直线和圆的交点，作出圆和圆的交点。

 
    作出过两点的直线

    为了连接 AB ，首先找出 AB 的中点 C ，然后找出 AC 的中点 D ， BC 的中点 E ……如此下去，直到 AB 之间有足够多的点，相邻点的距离都小于单位长度。这样，我们便可以用火柴棒连接很远的两点了。

 
    作出直线和圆的交点

      

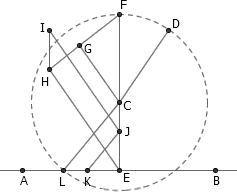
    如图，给定点 A 、点 B 、圆心 C 以及圆周上一点 D ，我们需要找到直线 AB 与（隐形的）圆 C 的交点 L 。过 C 作 CE⊥AB 。在 CE 的反向延长线上截取 CF=CD （这是可以办到的，比如先作 ∠DCF 的角平分线，再过 D 作角平分线的垂线；后面还会反复用到这个技巧）。向任意方向作单位长度线段 FG 。过 E 作 CG 的平行线，交 FG 延长线于 H 。过 H 作 EC 的平行线，截取 HI=HG 。作 IJ∥HE 。最后，利用公理 4 作单位长线段 JK ，则过 C 平行于 JK 的直线与 AB 的交点就是所求点 L 。
    为了证明其正确性，我们只需要说明 CL=CD 。图中的一系列平行线和等长线段告诉我们， CE:CD = CE:CF = HG:GF = HI:GF = JE:GF = JE:JK = CE:CL ，因此 CL 是等于 CD 的。

 
    作出圆和圆的交点

      

    如图，已知圆心 A 和圆周上一点 B ，圆心 C 和圆周上一点 D ，我们想要找出这两个圆的交点。由于我们已经能作直线与圆的交点了，因此为了作出两圆的交点，只要能找出公共弦所在直线即可。而公共弦与连心线垂直，因此我们只需要找出公共弦与连心线的交点 L 即可。不妨把圆 A 的半径记作 a ，把圆 C 的半径记作 c ，再在连心线上找出 LK=LC ，则由勾股定理可得 a^2 – AL^2 = c^2 – CL^2 ，即 (a+c)(a-c) = AC·AK 。也就是说， AK 就等于 (a+c)(a-c)/AC 。我们将利用这个关系找出 K 点来。
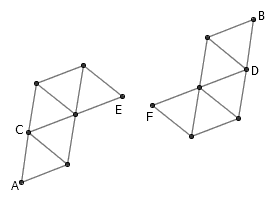
    过 C 作 AB 的平行线，截取 CE=CD 。作 EF∥CB ，则 AF 就等于 a+c 。过 B 作 AC 的平行线，截取 BG=BF 。截取 AH=AB ，然后作 BI∥GH ， AI 就等于 a-c 。作 IJ∥CF ，则 AJ 就等于 (a+c)(a-c)/AC 。最后，只需要截取 AK=AJ ，再找出 CK 的中点 L ，问题就圆满解决了。

 
    这样一来，所有尺规作图能够办到的事情，只用火柴棒也能办到，一切火柴棒作图问题都被终结掉了。不过，对火柴棒几何的研究还远未结束。如何简化作图过程，作出指定图形最少需要多少根火柴棒……这些悬而为解的问题都还有待人们继续探索。