在机器时代,作为机械构造的理论工具,连杆系统曾一度成为数学界中最热门的话题。所谓连杆系统,就是一些刚性的小杆在端点处以转轴的方式相连,形成的一个机械装置。固定某些顶点的位置之后,其余的动点就能画出一些有趣的轨迹。比方说,固定线段 AB 的其中一个端点 A ,则顶点 B 将描绘出一个绕 A 点的圆周。


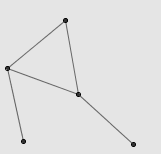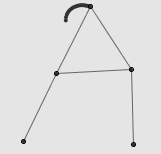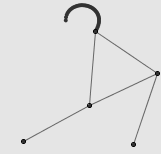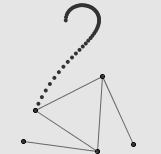
连杆系统最激动人心的,莫过于一些简单的连杆装置能够描绘出非常复杂的曲线。例如,上面的右图就是由五根相同长度的线段构成的连杆。固定 A 、 B 两个端点后,显然 C 和 D 描绘出的都是圆弧,但 E 点的轨迹就很难以想象了。事实上, E 点的轨迹相当的诡异,需要用一些复杂的代数语言才能描述。
在连杆系统领域中,有一个困扰人类近百年的难题——利用连杆系统是否能画出直线来?当时看来,这个问题是如此的困难,以至于人们普遍猜测甚至试图去证明,能画出直线的连杆压根儿是不存在的。 1864 年,一位法国海军军官 Charles-Nicolas Peaucellier 发明了第一个能画出直线的连杆系统,在当时引起了极大的轰动。 Peaucellier 连杆的原理并不难理解,利用初中几何知识足以证明 Peaucellier 连杆的正确性。
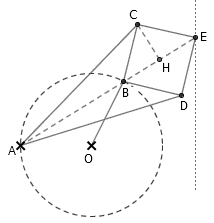
Peaucellier 连杆是由 7 根连杆组成的,其中 AC=AD=a , BC=CE=ED=DB=b , OB 为任意长。固定 A 点和 O 点的位置,使得 OA 的距离恰好等于 OB ,则 E 点将会描绘出一条垂直于 AO 的直线来。容易看出, A 、 B 、 E 三点在同一条直线上。我们首先说明, AB·AE 是一个常数。过点 C 作 CH⊥AE ,垂足为 H 。于是 AB·AE = (AH+HE)·(AH-HB) = AH2 – BH2 = (AC2 – CH2) – (BC2 – CH2) = a2 – b2 = 常数。
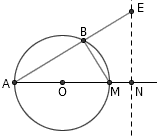
为什么 AB·AE 为常数,就能保证 E 点的轨迹是一条直线呢?过 A 点作出圆 O 的直径 AM ,在射线 AM 上找出一点 N 使得 AM·AN 也等于这个常数。由于 AM·AN = AB·AE ,我们立即可知 △ABM∽△ANE ,因此 ∠ANE = ∠ABM = 90° ,也就是说 EN 与 AN 始终垂直。这就证明了, E 点的轨迹确实是一条与 AO 垂直的直线。
解决了连杆画直线的问题后,数学家们显然还不满足。很多迹象都表明,连杆系统比我们想象中的更强大,画出一些更奇怪的图形似乎不成问题。
有一个非常简单的构造几乎是瞬间增强了连杆系统的功能,让人们更加相信构造复杂连杆的可能性。虽然连杆系统要求杆与杆必须在端点处连接,但我们可以利用三角形的稳定性,把某根杆的一端直接接到另一根杆的中间。如下图,虽然 AB 和 BC 是两根各自能绕着 B 转的连杆,但简单地用三角形固定一下, AB 和 BC 将会变成一条线段 AC 。利用这一基本构造,我们就能把连杆的端点直接连在另一根连杆的中间了。
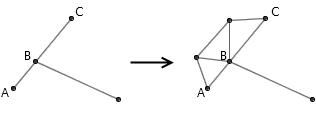
这一基本构造极大地激励了我们——我们何不像研究尺规作图一样,借助最基本的构造,构造出更实用的基本构造,逐渐搭建起连杆作图的大厦呢? 1877 年,英国数学家 Alfred Kempe 顺着这个思路研究下去,最后得出了一个惊人的结论:连杆系统不仅能画出直线和圆,还能画出双曲线、抛物线、椭圆,甚至半立方抛物线、双纽线等复杂的曲线。事实上,任何代数曲线 f(x,y) = Σ(i=1..n) Σ(j=1..n) Ci, j · xi · yj = 0 都是可以用连杆系统画出的!
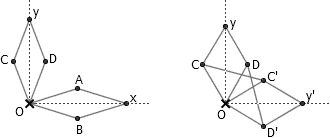
这个证明的基本思路是这样的。首先,以 O 为端点构造两个菱形。利用 Peaucellier 连杆,我们可以让 x 点和 y 点始终沿着两条垂直的直线运动。固定 O 点后,我们就建立起了一个平面直角坐标系。接下来,我们需要把 y 点绕着原点顺时针旋转 90 度。假设菱形 OCyD 的边长为 l ,则构造连杆 OC’ = C’y’ = y’D’ = D’O = l , CC’ = DD’ = √2 l ,这样我们就把 Oy 的长度转移到了 x 轴上。接下来,我们将用一系列连杆构造出一个点 T ,使得 T 始终在坐标系中的 (f(x, y), 0) 的位置上。然后我们将构造出一个点 S ,使得 S 始终在坐标系中的 (x, y) 位置上。最后,我们把 T 点的位置固定在 (0, 0) ,则 S 点就将描绘出 f(x, y) = 0 的图象来。
为了得到 T(f(x, y), 0) ,我们只需要实现对 x 轴上的点的以下四种操作:
(1) 把某个点的坐标加上一个常数 c
(2) 把某个点的坐标乘上一个常数 c
(3) 把两个点的坐标相加
(4) 把两个点的坐标相乘
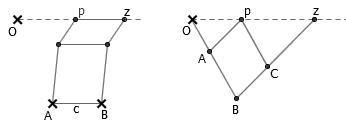
前两个操作并不困难。对于 x 轴上的某个点 p ,为了得到点 z=p+c,只需要固定两个距离为 c 的点 A 、 B ,并构造一系列平行四边形即可。为了得到点 z=c·p,我们只需要构造一组相似三角形 OAp 和 OBz ,使得 OB=c·OA , Bz=c·Ap 。添加一个连杆 pC 使得四边形 ABCp 为平行四边形,以保证这两个三角形是相似的。注意,在乘法器的构造中,我们用到了前面所说的基本构造,即连杆中间直接连接另一根连杆。
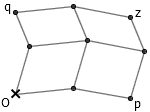
把两个变量相加也比想象中的容易。事实上,我们不但能在 x 轴上对两个动点做加法,还能直接实现一个更强的基本操作——对平面上的两个向量进行相加。只需要构造一系列的平行四边形,容易证明向量 Oz 即是向量 Op 和 Oq 之和。
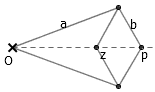
但是,对 x 轴上的两个变量进行相乘就有些麻烦了。注意到,由于 p·q = ((p+q)2 – (p-q)2) / 4 ,因此只要我们能实现平方操作,也就有了实现乘法的方法。而由于 1/(p-1) – 1/(p+1) = 2/(p2 – 1) ,因此只要我们能实现倒数操作,也就有了实现平方的方法。在证明 Peaucellier 连杆的正确性时,我们已经证明了,在上图中的连杆中有 z·p = a2 – b2 ,利用它我们便能实现 z = (a2 – b2)/p 。取 a 、 b 为适当的值,我们就能得到 p 的倒数了。
由于 x 和 y’ 都已经在 x 轴上了,利用上面的这些基本操作,我们便能得到 T(f(x, y), 0) 。另外,利用向量加法器,我们可以得到 Ox 和 Oy 的向量和 S = (x, y) 。将 T 点的位置固定在原点 O 处, S 的轨迹就是 f(x, y) = 0 的图象了。
Kempe 的结论最令人惊讶的地方莫过于,由于各种曲线都能用代数曲线近似地描述,因此连杆系统几乎可以视为万能的了。因此,如果你足够有耐心的话,你甚至能构造一个连杆系统,它能签出你的大名来!