用一张日落照片估算出地球的半径

    你相信吗，仅仅利用一张日落的照片，你就能得出地球的半径大小！ Princeton 大学的 Robert Vanderbei 在最近的一篇论文中对一张摄于密歇根湖的日落照片进行了分析，不但证实了地球是圆的，还依据照片上的内容对地球半径进行了估算。我把计算的大致过程向大家描述一下，供大家膜拜。

  

    事情的起因就是上面这张很平常的日落照片，以及这样一个大家平时并没有太在意的问题：太阳露出水面的部分应该是一个标准的弓形，但为什么在日出日落时，我们所看到的太阳是一个橄榄球一样的形状？大家或许会很快想到，发光体的下半部分其实是日光反射在水面上造成的。随之产生的是另一个问题：为什么它的下半部分要比上半部分小一些呢？


  

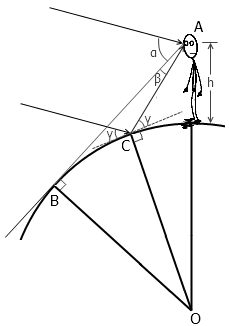
    这是因为——想到这个问题的答案并不容易——地球是圆的。上图就是人站在地球上看日出的一个比例夸张版示意图，其中 O 为地球的中心， A 为人眼的位置， AB 为视平线， B 点为水天交界处。由于太阳距离我们相当遥远，因此我们把太阳光看作是一束理想的平行光线。我们把直接射入人眼的太阳光与 AB 的夹角记为 α ，把经过水面上的一点 C 反射进入人眼的光线与 AB 的夹角记为 β 。从图上可见，视角 β 比 α 小，也就是说太阳在水面上的镜像比本身要小一些。

 
  

     β 究竟比 α 小多少呢？对照片进行精确地测量，可知太阳的直径相当于照片中的 317 个像素，而露出水面的部分高 69 像素，水中的倒影则只有 29 像素。众所周知太阳的视直径（看太阳的视角）为 0.5 度，因此我们就得到 α = 0.5 * 69 / 317 ≈ 0.1088 度， β = 0.5 * 29 / 317 ≈ 0.0457 度。
    如果再已知人眼（或者说相机）离水面的垂直距离 h 为 2 米，那么根据这些数据我们就足以估算出地球的半径了。不妨把 ∠AOB 记为 φ ，把 ∠AOC 记为 θ ，把人眼到水天相接处的距离 AB 记为 D ，把人眼到反射点的距离 AC 记为 d ，入射角和反射角记为 γ ，最后用 r 来表示地球半径，那么此时我们一共有 6 个未知量。为了求解出这 6 个未知数，我们需要寻找 6 个不同的方程。这 6 个方程可以由以下 6 组等量关系得到：

  

 
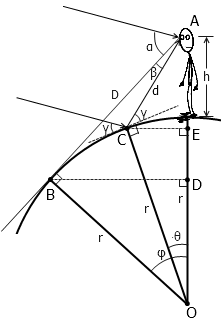
      1. 四边形 OBAC 的内角和为 360° ，即 (φ – θ) + 90° + β + (180° – γ + 90°) = 360° ， 化简得 方程(1) φ + β = θ + γ

      2. 两条平行线的同旁内角相加为 180° ，即 (α + β) + (180° – 2γ) = 180° ，即 方程(2) α + β = 2γ

      3. 由于 AO = h + r ，同时又有 AO = AD + DO = D·sinφ + r·cosφ ，因此有 方程(3) h + r = D·sinφ + r·cosφ

      4. BD 既可以等于 D·cosφ ，又可以等于 r·sinφ ，于是有 方程(4) D·cosφ = r·sinφ

      5. 由于 AO = h + r ，同时又有 AO = AE + EO = d·sin(γ+θ) + r·cosθ ，因此有 方程(5) h + r = d·sin(γ+θ) + r·cosθ

      6. CE 既可以等于 d·cos(γ+θ) ，又可以等于 r·sinθ ，于是有 方程(6) d·cos(γ+θ) = r·sinθ

 
    一系列复杂的代数运算（省略数百字）最终告诉我们：

      r = h / (√1 – 2·cosβ·cosγ + cos2γ / sinβ – 1)

    其中 γ = (α + β)/2 。代入已知的 α 、 β 和 h 可以得到，地球半径 r 大约为 7.29312 * 106 米，也即 7293 千米。

    这个估算的误差有多大呢？事实上，地球的半径大约为 6300 多千米，可见误差不是一般的大。不过，考虑到我们估算的依据仅仅是一张照片，能把数量级估对就已经相当牛 B 了。除了测量的精度之外，还有很多潜在的因素会导致误差。目前看来，误差的最主要来源似乎是不完全平静的水面——一点小小的波浪就会给 α 、 β 的值带来巨大的影响。

67 条评论

发表评论




Enter Captcha Here :