给出一个连续函数，某一点上的导数为正说明函数在这一点是上升的，换句话说函数从左边充分靠近该点时函数值总小于这个点，从右边靠近该点时函数值总大于这个点。但这并不等于说这一点左右是一个单增区间，也就是说该点左右任意小的邻域内函数都不是单调递增的。你能找出这样的函数来吗？
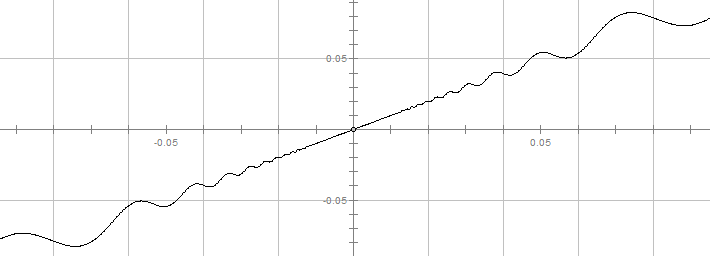
昨天数学课上，我学到了一个比较牛B的东西：函数上某一点导数为正，该点邻域不一定形成单增区间。虽然左边的点都比该点低，右边的点都比该点高，但这并不能说明左边和右边各自都是单增的。这样的函数确实存在，而且并不是那种很怪的函数，仅仅是一个简单的初等函数：f(x) = x + 2x^2*sin(1/x)。由于x=0时函数没有定义，我们规定f(0)=0。按照导数的定义，函数在x=0时的导数值为
Limit[ (f(0+Δx)-f(0))/(Δx-0), Δx->0 ]
= Limit[ f(Δx)/Δx, Δx->0 ]
= Limit[ 1 + 2Δx*sin(1/Δx) , Δx->0 ]
= 1
这说明函数在x=0处的导数确实是正的。当x≠0时，按照求导法则可以求出f'(x) = 1 – 2*cos(1/x) + 4x*sin(1/x)。当|x|充分小时，最后一项可以忽略不计；此时只要1/x恰好等于2πn (n为整数)，那么f'(x)保证是负的。这就告诉我们，x=0左右任意近的位置都存在导数为负的情况，这样不管邻域范围多小总能找到一个函数值在减小的地方。
其实，看一下f(x)的函数图象，你会立即明白这是怎么回事。这个函数越接近原点抖动频率越快（到原点时“周期”无限小），同时振幅也越小（到原点时振幅为0，这样可以保证导数存在）；但这个函数总的来说呈上升趋势。因此，这个函数才有我们前面提到的奇怪性质。
sofa~
……………….这个很好………………….
这个函数是干什么用的？
这个函数要是和我们数学老师说了 真的不知道他会什么反应。
认为扩充了定义域.
这个帅….
小疑问:
假如在第三象限曲线上的移动的一点p,在"最接近"原点的位置,点p是从"上"往"下"穿越原点的话,那么点p是不是从第二象限到第三象限,然后才穿越原点的呢?
第三象限的点"大体上"都是往上的,"局部范围"里有下降趋势,很难设想穿过原点的附近是单减的.我觉得应该是单增的,这样才能穿越原点,并且导数为1.
"某点导数是正的,这个点的邻域不一定形成单增区间",我的直觉不能接受这样的情形,无论这是不是真命题.
这是我的疑问
[cry]
回复：没有穿过第二象限。它在离原点任意近的地方都有一个递减区间，其幅度足够小以至于图象始终在一三象限。离原点越近幅度越小，最终将趋于0，此时导数为1。
其实这个函数很好想象。你可以认为这个图形可以无限放大，图象的样子不随尺度缩小而变化
第三象限任取一点p,与原点o连接做一段曲线段po,使得这段曲线段是从点p单调递减到点o的.这样的曲线段存在吗?
如果存在,那我就相信"函数上某一点导数为正，该点邻域不一定形成单增区间"
我转了您的，结果有同学说您求导求错了，我算的结果也是您错了。。。 不过我依然相信您是正确的。
http://hi.baidu.com/yuye%5Fabc/modify/blog/fd42274ef67bf8c9d1c86ad4
是不是高中数学知识有限？
回复：求导是正确的。只需要导数的乘法运算原则和复合函数的求导方法
您数学课研究这个？？？神牛啊
"你可以认为这个图形可以无限放大，图象的样子不随尺度缩小而变化"
传说中的分形??
回复：这个不是自相似的，应该不属于分形
导数不存在吧…
f'(x)=1+2*(2x*sin(1/x)-cos(1/x))
其实就是因为 sin(1/x),x->0 抖动很厉害
回复：x=0时需要按照导数的定义来求导，求出来的导数是存在的
地核
你给的链接看不了
更一般的情况，可以构造出点点连续点点不单调的函数~~~~
是我在一本数分小册子上看到的
还有一个简单的初等函数：f(x) = 0/(x-1) – x + x^3。由于x=1时函数没有定义，我们规定f(1)=76438910763。按照导数的定义，函数在x=1时的导数值为
这个matrix67牛帮忙求一下吧
回复：导数不存在，因为x=1时函数不连续
还有处处可导,光滑的,处处不单调的函数咧.就是图象不好画.
怎么我拿mathmatica画出来的图不大一样呢
哦，抱歉，函数打错了。
这种现象很常见，导函数在0点不连续引起的，不具保号性，从而改点的邻域不形成单调区间
“一个连续函数，某一点上的导数为正说明函数在这一点是上升的”——应该是“在某点的邻域内导数为正，才说明函数在该点的邻域上升”，单独一点谈不到上升。
f'(x0)>0 即 lim[f(x1)-f(x0)]/(x1-x0)=f'(x0) x1->x0
由保号性 存在任意a>0使得 [f(x1)-f(x0)]/(x1-x0)>0,其中x1属于x0的a领域( x0-a<x1x0 f(x1)>f(x0)
x1<x0 f(x1)<f(x0) 没有说函数是增函数啊 只有动点x1与定点x0的关系不能推出是增函数的
20楼的可能正确 19楼的就是瞎说喽
主要是因为导函数在x=0处不连续造成的
之前一直以为“导函数在某点不连续，则该点不存在导函数”，看来我得重新啃一下导数的定义了。
“换句话说函数从左边充分靠近该点时函数值总小于这个点，从右边靠近该点时函数值总大于这个点。” 这句话有问题,因为这句话等价于说这一点左右是一个单增区间
其实f(0)>0只能说明:
对任意小的距离d>0,总存在 -d<x<0, 满足f(x)<f(0), (并不排除”同时存在-d<xf(0)”的可能,而这里的这个函数就是这个情况)
对任意小的距离d>0,总存在 0<xf(0), (同上。。。)
你是错的
你对的，我错了
你对的
你的求导不对吧
什么软件画出来的函数图象在没有定义的地方画圈？
在0点不连续，重新定义一下就连续了。在0点的导数值存在，因为左右导数相等且为1.
对的～
这个的根本原因还是在于该函数的导函数在x=0处是震荡的。所以在x=0处虽然有导数值，但是在任意邻域内导函数在x=0处不连续，所以不具备保号性。
这个函数零点符合要求吗？ f(x) = sin(x)，如果x是有理数；f(x) ＝ x，如果x是无理数。
错了 。。可导必然连续！