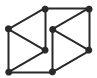
23. 一些硬币互不重叠地放在桌上。四色定理告诉我们，若要对硬币进行染色，使得挨在一起的硬币颜色不同的话，最多只需要四种颜色就可以了。存在至少需要四种颜色的构造吗？

 

答案：存在。如图，若只允许三种颜色的话， A 的颜色必须与所有阴影硬币颜色相同， B 的颜色也必须与所有阴影硬币颜色相同， A 、 B 将会同色。

  

 
 

24. 将火柴棍视为边，其端点视为顶点，可以把用火柴棍拼成的图形看作一个平面图。试着用火柴棍拼一个所有顶点的度均为 3 的平面图。

 

答案：如图。

  

 
 

25. 圆周上有 2n 个等分点，每两点之间连一条边，构成一个完全图 K_2n 。是否存在一个 Hamilton 回路，使得图中经过的边互不平行？

 

答案：不存在这样的回路。把 2n 个顶点从 1 到 2n 顺次编号，并定义一条边的方向值为两端点的编号之和。显然，两条边平行当且仅当它们的方向值模 2n 同余。假设有一条 Hamilton 回路使得途中任意两边都不平行，则这些边的方向值只可能恰好为 1, 2, …, 2n (mod 2n)，它们的和为 1 + 2 + … + 2n = 2n^2 + n ≡ n (mod 2n) 。另外，由于这是一条 Hamilton 回路，因此整条路所经过的边的方向值之和为 2 * (1 + 2 + … + 2n) = 4n^2 + 2n ≡ 0 (mod 2n) ，矛盾。

 
 

26. 证明：对任意正整数 n ，从 1 到 10^n 中的总数字个数等于从 1 到 10^(n+1) 中数字 0 出现的次数。

 

答案：对于 1 到 10^n 中每个数，列出所有在中间插入一个 0 后可以得到的数，构成一个新的数列：

    10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 100, 101, 110, 102, 120, …

由于对于一个 k 位数来说，在中间插入一个 0 有 k 种方法，因此数列的总项数就等于 1 到 10^n 中的总数字个数。下面我们只需说明，数列的总项数也等于 1 到 10^(n+1) 中数字 0 出现的次数。这是因为数列中的所有数显然都不超过 10^(n+1) ，并且显然一个数有几个 0 ，它就在该数列中出现了几次。

 
 

27. 经过一个公共点的 n 个平面（但任意三个平面不过同一直线）把空间分为了多少块？

 

答案：以这个公共点为球心做一个球面，我们要求的即是球面被切分出来的区域数。在这个球面上利用 Euler 公式 V – E + F = 2 ，我们能很快求出 F 的值。由于每对大圆有两个交点，因此 V = 2 * C(n, 2) ；由于每个顶点的度都为 4 ，因此 E = 4V/2 = 2V。于是 F = E – V + 2 = 2V – V + 2 = V + 2 = n^2 – n + 2。
利用 Euler 公式还可以瞬间秒杀下面这个经典问题： n 个圆最多可以把平面分成多少块？由于每两个圆之间都有两个交点，因此顶点数 V = n(n – 1) ；由于每个圆被切成了 2(n – 1) 条弧，因此 E = 2n(n – 1) 。于是， F = E – V + 2 = 2n(n – 1) – n(n – 1) + 2 = n^2 – n + 2 。
注意到，上述两个问题答案是一样的。其实，这并不是巧合。把前一个问题中的球面从北极点投影到与南极点相切的平面上，你就会发现这两个问题其实是一回事。

 
 

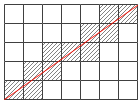
28. 证明：当 m 、 n 互质时， m×n 的棋盘的对角线恰好穿过 m + n – 1 个格子。

  

 

答案：由于 m 、 n 互质，显然对角线不会穿过交叉点。而从左下角到右上角必须要经过 m – 1 条竖直线和 n – 1 条水平线，因此对角线与棋盘必然有 m + n – 2 个交点，即它穿过了 m + n – 1 个格子。该结论可扩展为：对任意正整数 m 、 n ， m×n 的棋盘的对角线恰好穿过 m + n – gcd(m, n) 个格子。

 
 

29. 在空间中放置 8 个点，使得对于任意三个点，它们之间的三条线段中至少有两条一样长。换句话说，这 8 个点确定的所有三角形（包括退化成线的三角形）都是等腰三角形。

 

答案：在 x-y 平面作一个单位圆，标出它的五等分点。另外三个点放在 (0, 0, 0) 、 (0, 0, -1) 和 (0, 0, 1) 处。

  

 
 

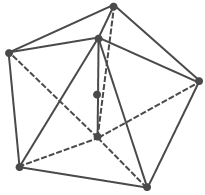
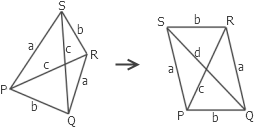
30. 证明：每组对边都相等的四面体中，每个面都是锐角三角形。

  

 

答案：把三角形 △PQR 和 △PSR 想象成是由转轴 PR 连接的两个三角形木板， QS 是一条橡皮筋。旋转 △PSR 使得 △PSR 和 △PQR 位于同一平面，橡皮筋 QS 将被拉长到 d 。此时，整个图形变成了一个平行四边形。由于对角线 d > c ，因此 ∠PQR < 90° 。同理可知，四面体中的每个角都小于 90° 。

  

 
 

31. 对于空间中的点集 E ，把所有点对确定的直线所构成的点集记作 L(E) 。如果 V 是一个正四面体的四个顶点，那么 L(V) 就是该四面体的六条边所在的直线所组成的点集。请问： L(L(V)) 是否包含了空间中所有点？

 

答案：不是。如图，设想一个由正方体六个面的对角线构成的正四面体。下面我们说明， P 点不在 L(L(V)) 中。首先，在四面体中相邻的边上取点，确定出来的直线始终在四面体的面上，不会过 P 点；在对边上取点构成的连线也不会过 P ，比方说同时过红色线段和蓝色线段的直线一定不会过 P ，因为过 P 且与红色线段相交的线都在正方体的顶面上。

  

可以证明，不在 L(L(V)) 中的点只有正方体中不在四面体上的那四个顶点。

 
 

32. 一幢大楼的底层有 1001 根电线，这些电线一直延伸到大楼楼顶。你需要确定底层的 1001 个线头和楼顶的 1001 个线头的对应关系。你有一个电池，一个灯泡，和许多很短的电线。如何只上下楼一次就确定电线线头的对应关系？

 

答案：对于奇数根电线的情况，都可以采用下面这种做法。在楼下把线头两个两个相接，余下单独一个线头什么都不接。把这个单出来的线头标号为 #1 。到楼顶找出和谁接都不构成回路的导线，它就是 #1 。在剩下的导线中测出能构成回路的导线对，并标号为 (#2, #3) ， (#4, #5) ，…… 。接下来，把 #1 和 #2 相接， #3 和 #4 相接，依此类推，让 #1001 单着。到楼下拆掉原有的连接，然后从 #1 开始顺藤摸瓜确定所有对应关系：和 #1 能构成回路的导线就是 #2 ，原来和 #2 配对的就是 #3 ，和 #3 能构成回路的就是 #4 ，依此类推。

 
 

33. 桌子上有 15 张大小形状任意的纸，它们完全覆盖了整个桌面。这些纸可能有重叠，也可能伸出桌面。证明：总能从中拿走其中 5 张纸，使得剩下的纸仍然覆盖了至少 2/3 的桌面。

 

答案：假设纸在放到桌面上之前，桌面上刷满了红色颜料。把纸覆盖上去后，某一些纸（的全部或某些部分）染上了颜色。由于整个桌面被完全覆盖，因此所有纸上的所有红色区域面积总和恰好等于桌面面积。如果我们拿掉颜料最少的五张纸，则拿走的颜料面积显然不会超过 1/3 ，也就是说纸上的红色面积之和还有至少 2/3 ，即还有至少 2/3 的桌面是被覆盖了的。

 
 

34. 即使钟的时针和分针一样长，大多数时候也能读出正确的时间来。例如，两针一个指向 12 一个指向 6 ，那么前者只能是分针，后者只能是时针。但有时候，时针和分针的位置互换后，所指的时间仍然有意义，我们就说这时的指针位置有歧义。从 0:00 到 12:00 这 12 个小时中，指针位置会产生歧义的时刻有多少个？

 

答案： 132 个。假设有 A 、 B 两个钟叠放在一起， A 以正常的速度运转， B 以 12 倍的速度运转。因此， B 的时针将永远与 A 的分针重合。每当 B 的分针与 A 的时针重合时， A 此时所指的时刻就是有歧义的。而 B 的分针比 A 的时针快 144 倍，因此 A 的时针转了一圈后， B 的分针转了 144 圈，因此 B 的分针与 A 的时针重合了 143 次。但是，这其中有 11 次是同一个钟的时针和分针本身就重合的，不会导致歧义，因此真正会导致歧义的有 143 – 11 = 132 个时刻。

 
 

35. Alice 和 Bob 玩猜数游戏。 Alice 背着 Bob 写下 n 个正整数 x1, x2, …, xn 。然后 Bob 选择 n 个正整数 a1, a2, …, an 告诉 Alice ， Alice 说出 a1·x1 + a2·x2 + … + an·xn 的值。接下来， Bob 又选择另外 n 个正整数 b1, b2, …, bn ，并获知 Σbi·xi 的值。如此下去，直到 Bob 能够推出 Alice 写下的 n 个数。 Bob 需要多少次询问就可以保证猜出所有 n 个数？

 

答案：两次。先选择 a1 = a2 = … = an = 1 ，从而获知 n 个数之和 S 。注意到，由于 Alice 写下的数都是正整数，因此对所有 i 都有 xi ≤ S 。然后，选择 b1 = 1, b2 = S+1, b3 = (S+1)^2, …, bn = (S+1)^(n-1)，然后 Alice 将告诉他一个数

    N = x1 + x2·(S+1) + x3·(S+1)^2 + … + xn·(S+1)^(n-1)

接下来， Bob 只需要把 N 写成 S+1 进制，每个数位上的数就依次是 Alice 的那 n 个数了。

下面我们证明，两次询问已经是最优的了，只问一次是猜不出来的。假设 Bob 第一次询问得到的结果是 a1 + a2 + … + an + a1·a2 ，则他没法知道 Alice 的 n 个数是 a2+1, 1, 1, …, 1 ，还是 1, a1+1, 1, 1, …, 1 。

 
 

36. 桌上有两个盒子，一个盒子里有 51 枚硬币，一个盒子里有 101 枚硬币。 Alice 和 Bob 轮流把其中一个盒子的硬币倒掉，再把另一个盒子里的硬币分装在两个盒子中。最后谁不能继续操作了，谁就输了。如果 Alice 先走，谁有必胜策略？

 

答案： Bob 必胜。 Alice 走后，两个盒子里的硬币数必然是一奇一偶。 Bob 倒掉有奇数枚硬币的盒子，把剩下的硬币分成 1 加另一个奇数。这样 Bob 面前总有一个盒子里有偶数枚硬币，因此他始终有走的。

 
 

37. 如果一个平面向量满足 y ≥ 0 ，我们就说这个向量是朝上的。两个朝上的单位向量，其向量和可能很小很小。证明：奇数个朝上的单位向量，向量和的长度不可能小于 1 。

 

答案：假设 n 个向量分别为 V1, V2, …, Vn 。注意到， V1 + V2 + … + Vn = V1 + (V2 + … + Vn) ，而两个向量的夹角变大将使得和向量变小，因此把 V1 变成 (1, 0) 或 (-1, 0) 中的某一个，那么这 n 个向量的和将会变得更小。反复利用该引理可知，这 n 个向量都是水平向量时，向量和最小。而奇数个单位水平向量的最小值为 1 。

 
 

38. 假设 n 次多项式 p(x) 满足，对于所有 x ，都有 p(x) ≥ 0 。证明，对于所有 x ，都有 p(x) + p'(x) + p”(x) + … + p^(n)(x) ≥ 0

 

答案：由于对于所有 x 都有 p(x) ≥ 0 ，因此 p(x) 的次数 n 一定是偶数，且最高次项系数大于 0 。令 q(x) = p(x) + p'(x) + p”(x) + … + p^(n)(x) ，显然 q(x) 的次数和最高次项系数跟 p(x) 一样，因此 q(x) 存在一个最小值，比方说 q(x0) 。我们只需要说明 q(x0) ≥ 0 即可。
由于 q(x0) 是最小值，因此 q'(x0) = 0 。而 q'(x) = p'(x) + p”(x) + … + p^(n)(x) = q(x) – p(x) ，因此 q(x0) – p(x0) = 0 ，即 q(x0) = p(x0) ≥ 0 。

 
 

39. 是否有可能在平面上画不可数个不相交的 8 ？

  

 

答案：不可能。对于任意一个 8 字形，在两个洞里各取一个有理点 P 、 Q （由于平面上的有理点是稠密的，这是总能办到的），则称这个 8 字形圈住了有理点对 (P, Q) 。注意到由于 8 字形不能相交，因此两个 8 字形不可能圈住同一对有理点。由于平面上的有理点对是可数的，因此 8 字形的数量也是可数的。