Mathematica 强大的符号计算和化简能力相信会让不少人震撼不已。输入 Sum[1/n^2, {n, 1, ∞}] ， Mathematica 竟然知道它等于 π^2/6 。我不禁问自己， Mathematica 真的什么都能化简出来吗？今天，我偶然遇到一个简单的表达式， Mathematica 竟然不知道它的精确值。
在 Mathematica 中输入 Cot[π/2] ， Mathematica 会告诉你它等于 0 ；在 Mathematica 中输入 Cot[π/4] ， Mathematica 会告诉你它等于 1 ；但在 Mathematica 中输入 Cot[π/8] ， Mathematica 返回的却还是一个 Cot[π/8] ，并没有给出它的值。而 Cot[π/8] 并不是一个复杂到无法用四则运算和平方开方表达出来的数。在一个边长为 1 的正八边形中，每条边的所对应的“圆心角”为 2π/8 = π/4 ，因此“圆周角” α 就等于 π/8 。由下图我们可以轻易看出， Cot[π/8]=√2+1 。
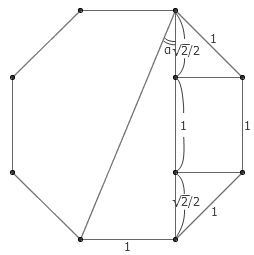
哈哈！我大笑，原来 Mathematica 也有做不到的事情！于是，我查了查 Mathematica 的帮助文档，想看看 Mathematica 对这个问题有何说明。万万没有想到的是，其实 Mathematica 并不是不知道 Cot[π/8] 等于多少，只是智能地保留了 Cot[π/8] 的形式。如果你愿意的话，可以用 FunctionExpand 函数将其展开，得到 Cot[π/8] 的精确结果。
Mathematica 真有那么无敌吗？不妨继续拿三角函数考考 Mathematica ，试探出 Mathematica 的极限。由于正十七边形可以用尺规作图作出，因此 π/17 的三角函数值理论上说是可以表示出来的。而无所不知的 Mathematica 也再一次给出了我们期待的结果：
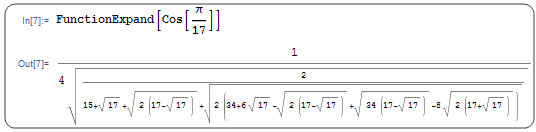
联想到正 65537 边形也能用尺规作图完成，这表明 π/65537 的三角函数值也能展开为用有限次加减乘除和平方开方构成的表达式。 Mathematica 还能算出 π/65537 的三角函数值吗？这下 Mathematica 似乎无能为力了。
由此可见， Mathematica 并不是万能的。 Mathematica 之所以能求出 π/17 的三角函数值，可能仅仅是因为它预先存储了这个值。
我又开始在想， Mathematica 化简不出，别的符号计算软件能把它化简出来吗？是否存在这么一个牛 B 的数学软件，输进去的任意表达式都可以化简成你想要的形式？后来我想到，这和软件牛不牛 B 是没有关系的。任意符号表达式的化简求值从理论上说就是一个不可能完成的任务。
首先，我们将说明化简求值至少是 NP-hard 的。我们下面将说明，我们能够把任意一个整数线性规划问题“编码”为级数的化简求值问题。例如，考虑下面这个整数规划问题：
最大化 x+y 的值，其中 x 、 y 满足：
x > 0
y > 0
x ≤ 5
y ≤ 5
2x + y < 12.5 x + 3y < 16.5
我们将考虑它的两个判定问题： x+y 是否能取到 8 ？ x+y 是否能取到 9 ？
为了把这个问题用一个级数表达出来，我们只需要用到这么一个函数： f(x)=x/√x^2 。这个初等函数有一个非常有用的性质：当 x 大于 0 时， f(x) = 1 ；当 x 小于 0 时， f(x) = -1 。因此， (f(a – b) + 1)/2 就可以用来判断 a 是否大于 b （假设 a 、 b 不相等）。如果 a 大于 b ，函数值为 1 ；否则，函数值为 0 。
为了判断出 x+y 是否能取到 8 ，我们只需要计算下面这个级数的值即可（我们用“大于 7.5 ”来代替“大于等于 8 ”，以排除分母为 0 的情况）。如果整个级数的值为 0 ，表示级数的每一项中的各个因式里至少有一个为 0 ，换句话说不管 x 和 y 取多少，这些限制条件中总有一个不成立。反之，如果整个级数的值为一个正整数，那么这个正整数就表示符合要求的解有多少个。 Mathematica 告诉我们， x+y≥8 有一组解，但 x+y≥9 是没有解的。
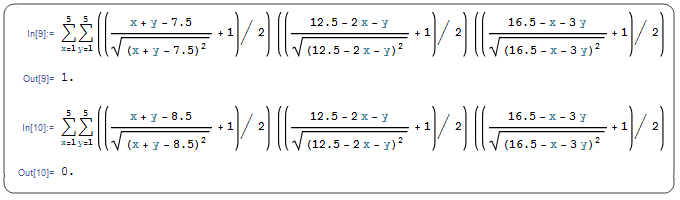
然而，整数规划问题是 NP-hard 的，因此级数的化简求值不会有什么有效的算法。
事实上，实际情况可能更糟：一般的级数很可能根本没办法化简求值。考虑定义在整数范围内的函数 g(x) = (f(x + 0.5) + f(x – 0.5))/2 。容易看出，当 x 为正整数时， g(x) = 1 ；当 x 为负整数时， g(x) = -1 ；当 x 为 0 时， x+0.5 和 x-0.5 一正一负，因此 g(x) = 0 。利用函数 g(x) ，我们就能构造出函数 isNonZero(x) = (g(x))^2 ，该函数的取值范围只有 0 和 1 ，并且函数值为 1 当且仅当 x 为非零数。另外，我们可以顺便定义出 isZero(x) = 1 – isNonZero(x) 。
考虑这么一个无穷级数：
Σ(a=1..∞) Σ(b=1..∞) Σ(c=1..∞) isZero(a^3 + b^3 – c^3)
如果化简求值的结果为 0 ，则表明对于所有的正整数 a 、 b 、 c ，a^3 + b^3 – c^3 都不为0。再把级数增强为
Σ(n=3..∞) Σ(a=1..∞) Σ(b=1..∞) Σ(c=1..∞) isZero(a^n + b^n – c^n)
如果哪个软件能瞬间求出它化简求值的结果，不就相当于证明了 Fermat 大定理吗？
鉴于 Fermat 大定理已经被证明过了，于是我开始着手构造一些更震撼的东西。考虑级数
Σ(a=2..n) Σ(b=2..n) isZero(a*b – n)
若级数值为 0 ，表明 n 不可能等于两个大于 1 的整数的乘积，也就是说这个数是一个质数。因此，可以定义
isPrime(n) = isZero( Σ(a=2..n) Σ(b=2..n) isZero(a*b – n)) )。
下面这个级数化简求值的结果为 1 当且仅当 n 能表示为两个质数之和：
canBeExpressedAsSumOfTwoPrimes(n) = isNonZero( Σ(i=2..n-2) (isPrime(i) * isPrime(n-i)) )
再考虑下面这个级数
Σ(n=2..∞) isZero(canBeExpressedAsSumOfTwoPrimes(2n))
如果级数不为 0 ，就表明存在某个 n 使得 canBeExpressedAsSumOfTwoPrimes(2n) 不成立。因此，如果有什么万能表达式化简软件具有化简这个级数的能力，我们就能够证明或推翻 Goldbach 猜想了。看来，计算机的符号运算也是有极限的。
当然，以上都是我个人的一些见解，我也不知道类似的话题是否有探究过，与此相关的还有些什么样的结论。如果大家发现了什么错误，或者想到了什么更牛的，欢迎加入讨论。
Update: 似乎有这样的结论：由于 Diophantine 方程是否有解是不可判定的，而它能规约到级数化简求值，因此后者也是不可判定的。感谢 24 楼的网友 DarkRaven 。
sf..
膜拜M67大牛
沙发？
首次前排，NP-hard威武
插入前排。
後面徹底暈了…
有没有m67的简历拿来膜拜一下。。。
传说中的规约？可算是见着了。有点机器证明的意思。
閣下的學術精神和學術能力真叫人佩服啊！
竟然可以用初等函数构造出isZero? 我一直以为不可以, 文中的那个当然不行, f(x) = x / x ^2 ^(1/2)定义域不包括零, 有更好的例子吗?
不算太晚 orz
你是怎么定义“任意符号表达式的化简求值”的？
没那么厉害吧，这都能求出来
@JimmyZ
这个isZero是定义在整数上的。f(x)是定义在非0整数上的。所以后面有f(x+0.5),f(x-0.5)这种处理。
这是否与某个希尔伯特问题有关，关于丢翻土方程求解的问题？？？
m牛之思考太NB了。。
不知你看过《mathematica全书》，里面说mathematica都符号计算都是系统的方法推导出来的，不是存储的，甚至于Pi也不是存储的值，而是一种方法，这种方法完全不同于手动的技巧，而是一种完全系统化的求解方法，甚至很多内部函数都是mathematica自己花了好几个月才推导出的。如果是值，那么多值（趋于无穷）怎么存储？？？
再说，matheamtica求解时，CPU常常100%运转好一会儿，如果是取值，我想不用那么夸张吧。。。就算是解压也没这么夸张，这么耗内存。。。
https://www.spoj.pl/FDULOCL1/problems/main/sort=0,start=0
Fudan University Local Contest #1 SPOJ 4412
Factorization, Factorization, Factorization
是一道模拟因式分解的题目… 我一直不会..记在这里了..###
膜拜。。。
你用的是7.x版本吧，5.x版本可以展开FunctionExpand[Cos[Pi/11]]，很长很长，其中含有i，我把展开结果反过来数值计算得到一个复数，虚部为0，但7.x却不能展开，难道是退步了？
退步了？可能是因为高版本考虑到这些展开对绝大多数人来说并无多大实际意义。其实sin(1 degree)等都可以展开的，详情参见：
http://zh.wikipedia.org/zh-cn/%E4%B8%89%E8%A7%92%E5%87%BD%E6%95%B0%E7%B2%BE%E7%A1%AE%E5%80%BC
这里面不少无法用mathematica展开
好强大！！！
要是可以用这种方式模拟图灵机就无敌了….
可以用这种方式判定任意丢番图方程是否有解,而这个判定问题是不可解的….
所以级数化简求值也是不可解的??
就是这样…
有一丢番图方程P(x1,x2,x3…)
用Σ(x1=-∞..∞)Σ(x2=-∞..∞)Σ(x3=-∞..∞)….isZero(P(x1,x2,x3…))
就可以了
丢番图方程就是图灵机吧。。。
这样的图示是自动生成的么？？
@26楼
所以我说这个化简问题不可解。。。。
不过Wolfram|Alpha能化简出来。
In[33]:= RootReduce[Sin[[Pi]/257]]
Out[33]= Root[
257 – 2829056 #1^2 + 9341542912 #1^4 – 14684905457664 #1^6 +
13461163336192000 #1^8 – 8072782026926489600 #1^10 +
3411681881225702604800 #1^12 – 1070293344453091845734400 #1^14 +
259010989357648226667724800 #1^16 –
49802814795786395864530944000 #1^18 +
7789160234060992313212639641600 #1^20 –
1009943131692240283962954271948800 #1^22 +
110285789980792639008754606496808960 #1^24 –
10278258580774042185909916489241067520 #1^26 +
826817549872118763034034168814318387200 #1^28 –
57973246012968946559057311914025885368320 #1^30 +
3573260072435722342458259770700868207247360 #1^32 –
195057961601197078458897945130023864489738240 #1^34 +
9492820797924924484999699996327828071833927680 #1^36 –
414302057496480509912132655710178083458986803200 #1^38 +
16301270223251764843664692687601445956976524656640 #1^40 –
580996767292508083863238615124878113709116799057920 #1^42 +
18838380030393443931323191460109684292992574999756800 #1^44 –
557866994942604002895021281240546913586751443933593600 #1^46 +
15142104148442108650007720490814844797354682049626112000 #1^48 –
377946919545115031904192703450738526141972863958667755520 #1^50 +
8701007311791893521138323167105391149004315773748023132160 #1^52 –
185269933467245571136965507436951156990920178293543765278720 #1^54
+ 3658036430714186991020085883679952919234258557886059606179840 #1^56
– 67131703053433940104050670220660737383960092763075553263616000
#1^58 + 11476219662970641432869514574771314253113702415300850318573568
00 #1^60 –
18312591376181109555245547988129710055506166004630604164261478400
#1^62 + 27328020976762578874751048536132028852063047729987209291282513
9200 #1^64 –
3820731725163658245935343339434252717661569115465240224387720806400
#1^66 + 5012878196953853401956089854551845637238836205201197532252943
1552000 #1^68 –
6181675632493114030162672736534678378573315761456156828102985515008
00 #1^70 +
7175260026391550623138590911539339012937611262840890710976159442534
400 #1^72 –
7850122320765674843909463786462498466046337943778358269738241465778
1760 #1^74 +
8105532999144653738352451124969412291735883867307989065117284728779
57120 #1^76 –
7908222069272583296815147056688754738383014250284912408225432617562
931200 #1^78 +
7298996072824917620616054246395695114092767226559259896776954845543
2683520 #1^80 –
6379704354690107249709195342485852350090369332553001068755032175311
16584960 #1^82 +
5286040751028946006901904712345420518646306018401058028397026659543
537418240 #1^84 –
4155921693912412722667704394533640959487440593777383553360420959916
9880391680 #1^86 +
3103144799029595199458725140351472463110642567978822653224175405208
70097715200 #1^88 –
2202437129157415259513269535510993789202630417478302847211414749132
739565322240 #1^90 +
1487031183697587245343180861704056676188143454381563801749754642682
3293502750720 #1^92 –
9558296746275644779697489525398975723762534633986759487170875306827
0665963929600 #1^94 +
5853225017822405153752895647512362453520562445967149624102577249747
70882294579200 #1^96 –
3417096114300773324145166042827254270948306090904755253650484182907
753326444544000 #1^98 +
1903018041952375227094230688880667309230696247536739341656756775447
4783079787397120 #1^100 –
1011610047658064455385099900177113153302074281671728714571164595423
47961682844712960 #1^102 +
5135866395802481081185891800899189855225915583871853473976681792149
97343928288542720 #1^104 –
2491588014130098033954968351725242660853031027040776455229174210291
484204929478819840 #1^106 +
1155629507063399190060663200851157401313077591542867774851451850848
7515935197888512000 #1^108 –
5126792722244898224996396745594225562188926042481086128431895483765
3707057968814489600 #1^110 +
2176456379430893582748154269494994872039243192244182960717358411439
20541467331579084800 #1^112 –
8845278100387338679543986230258834994832256085642263016553841049693
42978594921932390400 #1^114 +
3442697983899652066078923729938054080216763155525839239511052900154
772583355301809356800 #1^116 –
1283717892301565177181971560315884572284216769857092597783782437345
8474039629938950144000 #1^118 +
4587434848191708947218880187442880074840457283357081316377748148002
8464254016409934233600 #1^120 –
1571577040356120042373905055818096620601081087717052087913816318756
03311366818312801484800 #1^122 +
5162884057737653713398660996274676123935938644293696278488485609745
62620309573450829135872 #1^124 –
1626879550852165047146694676141446499645955319334241601965400564840
729006779773258630692864 #1^126 +
4918473060715847816955123439497396394278469570080265308267490079751
041183287686595860234240 #1^128 –
1426963693387249612096997879616484797701178065287878733710394303349
0278495823723976997208064 #1^130 +
3973650093547269254739008449458345226134381023911700588609806146168
1062605595250500537679872 #1^132 –
1062275945406002991482467930435630597765940665098782976590216833768
32293400032410956661260288 #1^134 +
2726614685116825196686214378765221001908455687402543853180041319135
69536258219730656471023616 #1^136 –
6720589214488765264275060777187970439486590809112307026293001437219
04268287385510657801584640 #1^138 +
1590879902809680968941464235037687349018892681500505991512762771825
589799824364242250139435008 #1^140 –
3617046358362914949969936019069238133039704388826719226640462506138
275873056793476617966977024 #1^142 +
7899296644700618856256182110610979830776365906633064977720550300761
751906675755868476019834880 #1^144 –
1657151859710188535011081648253418860781265019943374883780123272488
5710457840333250501552373760 #1^146 +
3339553267074223584976077836404041999506594299214746047305853357037
5520258771286488857654067200 #1^148 –
6465021265106867803709980616805493756925613546665262016877132803504
7497232079618982932910178304 #1^150 +
1202267112458470152970627974353302347779149185871083813664870310827
19907133341045827910324191232 #1^152 –
2147661067248813042424280554102421956820398880835484449713869713182
73013831824976711440981295104 #1^154 +
3685011787116777694546707741531936155210699108616299139097487376563
41055580132811584255912050688 #1^156 –
6072744526177636993640382951175151533545217064593375700924925459347
39260449705373759581034905600 #1^158 +
9610778293602868981239562583598935470480256571791255457115968987836
74307842142417602119550894080 #1^160 –
1460506367362326465497164157216761654773277799412404373942094991834
858843637411608480567043031040 #1^162 +
2130849644621753468508057683921572436454139228411002390363411318464
162126637287889978299588280320 #1^164 –
2984204119572720462497540997062662444011813772593202395334719032827
812942953829631358397778493440 #1^166 +
4010891420220308990169983250489968965324415805936763997110907237697
567691713093080185843168051200 #1^168 –
5172352857283073389181022775864050793673261084725057059638585845435
377283348484120743271024558080 #1^170 +
6398170586465767082570744936617958785237444347578972316547152433081
911784026448565543699417661440 #1^172 –
7589554074980082332428745717919233869385106398507470609973173920621
302254155511401886319309225984 #1^174 +
8630340381102158337954413466601532504786145642678757026440989758734
238926913355030188141217579008 #1^176 –
9404476116749323253210006765438616802654415187803855500534529044732
056228185038184926629309972480 #1^178 +
9816679673984376463940021794936662990321404288116437012344329765293
056114429612602608496303669248 #1^180 –
9811374316567342933154249850172690735057314175908843910013752754070
595446380019945824524859080704 #1^182 +
9384792824542675849104065074078225920489604863912807218274024373458
830426972192991658241169555456 #1^184 –
8586672613657814853139203234933743364201632602758932117599693854894
882971305936109669710395604992 #1^186 +
7510801104145133559483463822518877174360766106432162845181765310428
148225492189977725278596628480 #1^188 –
6276868996597233689501639316873863514577385353427242622448955038155
549170094437521202872672321536 #1^190 +
5008486142362559524265556760614378141165374841594794631384140289512
717990645302478058250733355008 #1^192 –
3812963280466341905864341387937988116985535168858844445780154383768
603704218469769179952977018880 #1^194 +
2767390525530632072152240315331352403149348326222424550620093402329
103651896260147402336119029760 #1^196 –
1913195216371108513411172686402366363681748347959465122554472978007
329157851229034445957968691200 #1^198 +
1258711121457290496584544656964422527031215928030645113465689087620
344317583316057289221302386688 #1^200 –
7872853446602103754670146164420696720796133766309804874937324713282
59061049038926921766277218304 #1^202 +
4676271631123774683548695139268534350659396526904245650249716544187
93760795268458745496755765248 #1^204 –
2634556298159503845916557666755482135927989826048205935500192070202
40638556951584186994373165056 #1^206 +
1406001704943423105108210753329204673204116763993337727815707950604
89115166573351884851616153600 #1^208 –
7097595607351498085096018535424881545978263095690132768174623209011
5561454432695440315074478080 #1^210 +
3383759372731487527149151542001657585300293381256470418842751537859
8808729538202397003785175040 #1^212 –
1520889889764989394945543444655385326320583940977696332572660330426
9145066873506315367056670720 #1^214 +
6432437526604614645289395213954676290531501972593841119841359103597
702931509224893237679882240 #1^216 –
2554543494290634947733378016349978267950175472338386067449879950655
867948167544383892304691200 #1^218 +
9503616356381942602756343389497821248597855603384764950233119816426
02621276317211350144122880 #1^220 –
3303402219137487745086073547579657173794527920313599064024795495516
88803517207339977240739840 #1^222 +
1069673099530234126980252386835317561038228088482498744541362350929
27803043667138659297001472 #1^224 –
3215983370463984089225256873912895805515112478412939190637006919951
1099648074576949845950464 #1^226 +
8943552926365021254797887422281323660476410247942211952817233677639
262370528668836891197440 #1^228 –
2290680749519578566446257331872844953355222861923538871709710443917
091705969398184310472704 #1^230 +
5376675549412537526097031416827485712625992983588475137681812585544
63141285698611856801792 #1^232 –
1149840052029304260900183478121317184587773731351163259122351627677
84807083466369802436608 #1^234 +
2225178560245510498459484010438592792315322689720551941060633272184
9795320593577678995456 #1^236 –
3864977352277635055866478327613884319833231632931165074659656258427
551382993997177815040 #1^238 +
5965857157872532119428754928930974966713535964524453974163452813838
37806835587946119168 #1^240 –
8083520360835346040813576722396015463519616121710514108447163898354
6230739481766395904 #1^242 +
9465480516200639392053368527395802650491353772494747199586842972312
205004623157657600 #1^244 –
9384163561040231015721913697546544742859009763587169140303337952208
40705504260915200 #1^246 +
7659053042434700790134480670364455483872491451042773103240190322439
8192054370304000 #1^248 –
4940852066259070724854880916913994549596150660369903668831281342667
153489021370368 #1^250 +
2362086250385477064018708362311602890264299393438651481052410052771
42289894866944 #1^252 –
7439641733497565555964435786808198079572596514767406239535149772508
418579365888 #1^254 +
1157920892373161954235709850086879078532699846656405640394575840079
13129639936 #1^256 &, 129]
In[10]:=
Cos[Pi/65537.0]
Out[10]=
1.
In[11]:=
Cos[Pi/65537]
Out[11]=
!(Cos[π/65537])
东西方人思维到底有什么本质不同？为什么中国人只能发明算术，而西方人却能发展出这么美妙的技巧。
其实搞掉Mathematica很简单…
In[4]:= Sin[0.5 Pi + Pi/2]
Out[4]= 1.22465*10^-16
呵呵
凡是加了个小数点之后mathematica就萎了。。
楼上去看看Mathematica的精度控制相关内容
用 Simplify`TrigToRadicals[Cos[Pi/65537]] 可以解决你的问题。
忘了说了，关于 Mathematica 的问题，在 http://groups.google.com/group/comp.soft-sys.math.mathematica/topics?pli=1 可以得到较好较快的解答。
sin or cos 一个有理数都是代数数
单位 度
Cot[π/8]//N
楼主说:Mathematica 强大的符号计算和化简能力相信会让不少人震撼不已。输入 Sum[1/n^2, {n, 1, ∞}] ， Mathematica 竟然知道它等于 π^2/6 。我不禁问自己， Mathematica 真的什么都能化简出来吗？今天，我偶然遇到一个简单的表达式， Mathematica 竟然不知道它的精确值。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
楼主的这个错误太低级了吧. 建议你少用一些”震撼” “神奇”等词语,另外blog中如果是转载摘抄的内容最好还是留下出处…..
LS搞清楚了
M67大牛的都是原创的….
In[100]=N[Cot[[Pi]/8]]
Out[100]=2.41421
mathematica一般给解析表达式，不会主动化成小数。
要看数值结果，加个 N[] 不就可以了。
请问一下你贴的那些英文网站我都看不懂怎么办。 我用了一些翻译的软件，可是他们翻译的。。。没法说。。
思维挺不错的，支持你！
如果有用来解停机问题更
支持
其实很多必须使用坐标变换而直角坐标求不出最终结果的二重积分, 如绝大多数极坐标情形, 如果用mathematica直接在直角坐标系下定限, 限好定, 但是mathematica也是求不出数来. 如
!(
*SubsuperscriptBox[([Integral]), (-1), (1)](
*SubsuperscriptBox[([Integral]), (-
*SqrtBox[(1 –
*SuperscriptBox[(x), (2)])]),
SqrtBox[(1 –
*SuperscriptBox[(x), (2)])]]
*SuperscriptBox[(E), ((-
*SuperscriptBox[(x), (2)]) –
*SuperscriptBox[(y), (2)])] [DifferentialD]y [DifferentialD]x
))
膜拜M67大牛
郁孤台下清江水，中间多少行人泪？
膜拜matrix67大佬
Mathematica免费公开课，在线直播
2021年01月15日 晚19:00-20:00
点击链接图片，扫码免费听课哦：http://www.uone-tech.cn/sms/