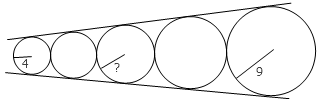我找到了这道经典智力题的出处。它似乎来源于一本叫做 Which Way Did the Bicycle Go 的书。这本书又是一本超赞的趣题集，里面有很多我没有见过的趣题妙解。我找到了这本书的电子版，并且传到了自己网站上，与大家分享一下。大家可以点击这里下载。阅读器可以在这里找到。

    我整理出了个人认为比较精彩的题目。如果你没有时间翻遍整本书的话，看看我精选出的这些题目也是一个不错的选择。

 

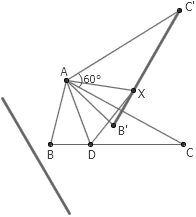
1. 给定 △ABC ，对于平面上的任意一点 X ，它属于点集 S 当且仅当线段 BC 上存在一点 D 使得 △ADX 是等边三角形。点集 S 是什么样子的？

 

答案：两条线段，它由线段 BC 绕 A 点顺时针或逆时针旋转 60 度而得。这是因为，给定 A 点和 X 点，则 D 点的位置可以由 X 点绕 A 旋转 60 度得到的。既然 D 点在 BC 上，那么显然 X 点就应该在 BC 绕 A 旋转 60 度得到的线段上。

  

 
 

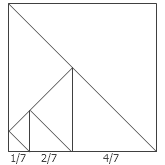
2. 能否把一个正方形分割成 7 个等腰直角三角形，其中任意两个三角形都不全等？

 

答案：能。如图。

  

 
 

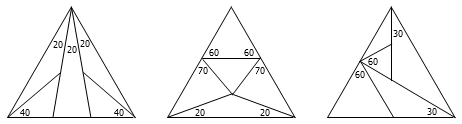
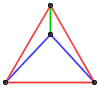
3. 能否把一个等边三角形分成五个等腰三角形，使得
    (1) 五个三角形都不是等边三角形？
    (2) 恰有一个三角形是等边三角形？
    (3) 恰有两个三角形是等边三角形？

 

答案：都可以。如图。

  

 
 

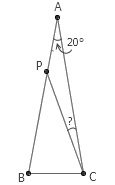
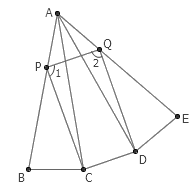
4. △ABC 中， AB=AC ， ∠A=20° 。 P 在 AB 上，满足 AP=BC 。求 ∠ACP 。

  

 

答案：把 △ABC 翻折两次，得到 △ACD 、 △ADE 。在 AE 边上截取 AQ 使得 AQ=AP 。显然 △APQ 为等边三角形，因此 AP = PQ = CD 。另外，由 SAS 可得 △APC 与 △AQD 全等，因此 PC=QD ，四边形 PQDC 是平行四边形。由全等还可得 ∠APC=∠AQD ，由此可知 ∠1=∠2 。也就是说，四边形 PQDC 事实上是一个矩形。因此， ∠ACP = ∠ADQ = 90° – ∠ADC = 10°。

  

 
 

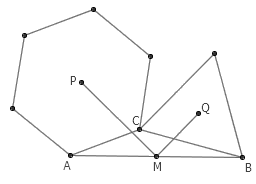
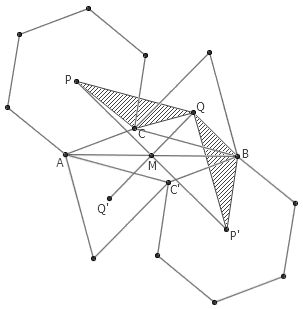
5. △ABC 中， M 为 AB 边的中点。以 AC 为边向外作正六边形， P 为其中心；以 BC 为边向外作正三角形， Q 为其中心。证明： ∠PMQ 为直角。

  

 

答案：把整个图形绕 M 点旋转 180 度，则四边形 PQP’Q’ 是平行四边形。下面我们证明两个阴影三角形全等。显然 CP=BP’ ，且 CQ=BQ 。另外，记 △ABC 的三个角分别为 α 、 β 、 γ ，则 ∠PCQ = 360° – 60° – 30° – γ = 270° – (180° – α – β) = 90° + α + β = 60° + α + β + 30° = ∠P’BQ ，于是 △PCQ≌△P’BQ 。因此， PQ=QP’ ，四边形 PQP’Q’ 是菱形，它的两条对角线互相垂直。

  

 
 

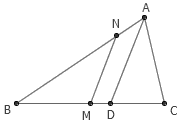
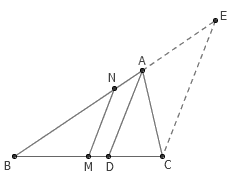
6. △ABC 中， AD 是角平分线， M 是 BC 的中点。过 M 作 AD 的平行线，与 AB 交于点 N 。求证 MN 平分 △ABC 的周长。

  

 

答案：过 C 作 MN 的平行线，与 BA 的延长线交于 E 。易证 AC=AE ，所以 △ABC 的周长就等于 BC+BE 。只需注意到 MN 是 △BCE 的中位线，问题即得证。

  

 
 

7. 五个圆依次相切，它们又都相切于两条不平行的直线。如果最左边那个圆的半径为 4 ，最右边那个圆的半径为 9 ，求中间那个圆的半径。

  

 

答案： 6 。下面我们说明，五个圆的半径成等比数列。把五个圆从小到大依次记作 C₁ 、 C₂ 、 C₃ 、 C₄ 、 C₅ ，把两条直线的交点记为 P 。把 C₁ 、 C₂ 的圆心到 P 的距离分别记作 P₁ 、 P₂ 。现在，把整个图以 P 为中心缩小到原来的 P₁/P₂ ，则两条直线还在原来的位置，但是 C₂ 现在占据了 C₁ 的位置。另外，由于所有相切关系都不变，因此新的 C₃ 就是原来的 C₂ ，新的 C₄ 就是原来的 C₃ ，新的 C₅ 就是原来的 C₄ 。这就说明，每个 C_i 缩小到原来的 P₁/P₂ 就和 C_i-1 重合，也就是说每两个相邻圆的半径之比为 P₁/P₂ 。

 
 

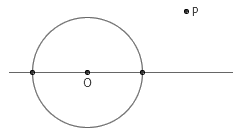
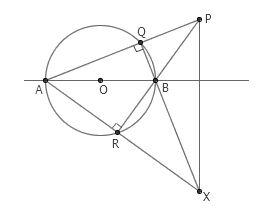
8. 给定一条直线和直线外一点 P ，再给出直线上一点 O ，以及一个以 O 为圆心的圆。如何只用一个没有刻度的直尺作出已知直线过 P 点的垂线？

  

 

答案：连接 AP ，与圆交于 Q ；延长 PB ，与圆交于 R 。则 AR 、 QB 的延长线的交点 X 就满足 PX⊥l 。这是因为在 △APX 中， QX 和 PR 都是三角形的高，说明点 B 是三角形的垂心，自然就有 PX⊥l 了。

  

 
 

9. 证明：把一个正 400 边形剖分为平行四边形，则其中至少有 100 个矩形。

 

答案：假设这个正 400 边形的底边是一条水平线段。显然，我们可以从最上面的边出发，穿过一个个平行四边形，一路走到最下面的边，使得路上经过的线段都是水平线段；类似地，正 400 边形的最左端到最右端也有这么一条通路，路上经过的每条边都是竖直线段。但这两条路径显然有一个交点，这个交点所在的四边形显然就是矩形。这个操作可以在该正 400 边形的不同方向上进行 100 次，因此我们能找出 100 个朝向不同的矩形。

 
 

10. 图中所示的是一种用不相交线段覆盖四边形中每一个点（包括边界上的点）的方法，其中每条线段的长度都不为 0 。是否有可能
    (1) 用长度都不为 0 的不相交线段覆盖一个三角形中的每一个点？
    (2) 用长度都不为 0 的不相交线段覆盖一个圆里的每一个点？

  

 

答案：都是可以的。如图。

  

 
 

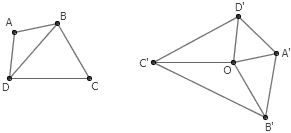
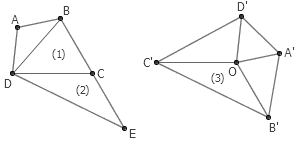
11. 给定任意四边形 ABCD 和四边形外一点 O 。把 AB 平移到 OA’ ，把 BC 平移到 OB’ ，把 CD 平移到 OC’ ，把 DA 平移到 OD’ 。求两个四边形的面积之比。

  

 

答案：倍长 BC 到 E ，于是三角形 (1) 和 (2) 面积相同。而显然三角形 (2) 和 (3) 全等，因此 (1) 和 (3) 面积相同。同理可知，右边这个四边形中的四个三角形事实上分别与 △ABC 、 △BCD 、 △CDA 、 △DAB 等积，因此右边这个四边形的面积是左边的两倍。

  

 
 

12. 图中的四个点之间一共有 6 条线段，它们满足：有一种长度恰好出现 1 次，有一种长度恰好出现 2 次，有一种长度恰好出现 3 次。是否存在平面上的五个点，它们之间的 10 条线段满足有一种长度恰好出现 1 次，有一种长度恰好出现 2 次，有一种长度恰好出现 3 次，有一种长度恰好出现 4 次？

  

 

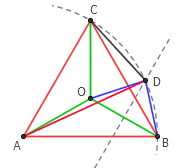
答案：是的。下图是一个简单的构造： △ABC 为等边三角形， O 为其中心。以 A 为圆心， AB 为半径作弧， OB 的中垂线与这段弧相交于点 D 。则这五个点满足要求。

  

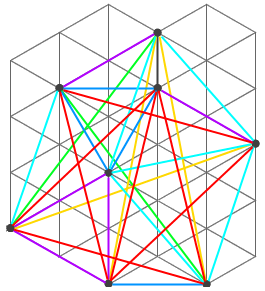
受很多与维度有关的几何命题的影响，或许很多人认为五个点已经是最多了吧。其实不是。现在已经发现了一些 n=6 、 n=7 甚至 n=8 的构造。下图显示的就是一个 n=8 的构造，构造出这玩意儿的人简直是太牛 B 了。

  

 
 

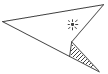
13. 如图，四边形房间内有一光源，它照亮了大部分区域，只有其中两面墙有阴影部分。是否存在这样的多边形房间，把光源放在房间里的某个位置后，能够让每一面墙都有阴影部分？

  

 

答案：有。如图。