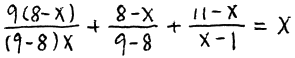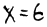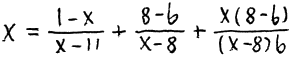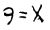Math Horizons的愚人节笑话：一个奇妙的分式方程

Math Horizons 杂志 2010 年 4 月刊上发表了一个有点搞笑的题目，很有些愚人节玩笑的味道。

    观察下面这个分式方程：

    它可以化简为 x^3 – 42x + 36 = 0 ，如果分式方程存在整数解，这个解一定是 36 的约数。把 36 的约数一个一个代进去便可得到，这个分式方程的唯一整数解为：

 
    现在，你能快速求解出下面这个方程的整数解吗？

    只需要注意到，新的分式方程是由原方程旋转 180 度得到的，因此它的解应该为：

有意思的是，这个“推导”虽然是荒谬的，但 x = 9 真的就是第二个方程的唯一整数解！
来源：http://www.cut-the-knot.org/proofs/FalseSymmetry.shtml

38 条评论

发表评论




Enter Captcha Here :