玩转内接多边形（四）：登山引理 一个无关的问题

    在继续探索多边形内接图形问题之前，我们先来看一个看似无关的趣题。从水平线上的一点起笔，在这条水平线上方随意画一条折线段，最后回到水平线上（如下图）。把这个折线段想象成一座座山峰。我们以最高峰所在位置为界把整座山分成左右两部分。现在，假设有一对相恋的登山者，一个站在最左侧的山脚出（即点 0 处），一个站在最右侧山脚处（即点 0′ 处）。这两个人将同时从山脚出发，同时到达山顶，并且保证在此过程中他们俩总处于同一海拔高度。不管这座山是什么形状，这种浪漫的想法总可以实现吗？

   

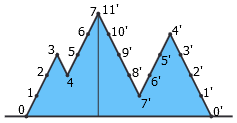
    注意，在登山的过程中，登山者可以为了照顾对方而走回头路。例如，对于图中所示的小山，两个人可以按照下列方法实现同步登山。左右两个人的路线分别为：

0 → 1 → 2 → 3 → 4 → 5 → 6 → 5 → 4 → 3 → 2 → 1 → 2 → 3 → 4 → 5 → 6 → 7
0'→ 1'→ 2'→ 3'→ 2'→ 3'→ 4'→ 5'→ 6'→ 5'→ 6'→ 7'→ 8'→ 9'→ 8'→ 9'→ 10'→ 11'


    事实上，不管折线段是什么样，这样的登山方式总是能实现的。就像本 Blog 之前介绍的矩形剖分问题一样，这个问题也有数学归纳证明、构造证明、图论模型证明等多种证明方式。下面我们给出一个拓扑证明，它是我所见过的最巧妙的证明方式。

  

    以左侧登山者所在位置为横轴，以右侧登山者所在的位置为纵轴。把所有位于同一高度的点对全部标在平面上，形成连续的曲线。下面我们只需要说明，这条曲线连通了最左下角的点和最右上角的点。为此，我们只需要说明任意一条从左上角到右下角的连续曲线必定会和这条曲线相交。而这是显然的，因为一个人从山顶走到山脚，另一个人从山脚走到山顶，他俩必然会有某一时刻在同一高度“相遇”。

28 条评论

发表评论




Enter Captcha Here :