当我们进一步考虑内接菱形时，情况有了一些变化——证明任意多边形内均存在内接菱形没有前几个问题那么容易了。但我们可以轻易证明一个弱化版的命题：任意凸多边形内均存在内接菱形。下面将给出这个命题的两种不同的证明，它们都相当经典。
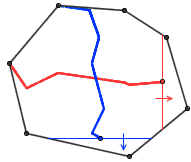
证明 1 ：考虑凸多边形内的一条水平线段由上至下扫过，这条线段的中点所形成的轨迹就是一条连接凸多边形最顶端与最底端的折线段。类似地，考虑一条从左至右移动的竖直线段，它的中点就构成了从凸多边形最左端到最右端的连线。显然，这两条连线会有一个交点，也就是说我们找到了两条互相垂直且中点重合的线段，它们对应的四个端点显然就是一个菱形的四个顶点。
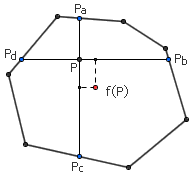
证明 2 ：考虑凸多边形内的任意一点 P ，过 P 点作水平直线和竖直直线，与凸多边形交于四个点 Pa 、 Pb 、 Pc 、 Pd 。令 f(P) 表示 Pa 、 Pb 、 Pc 、 Pd 的重心（也就是 Pa Pc 和 Pb Pd 的中垂线的交点）。由图形的凸性可知，这个重心一定位于凸多边形内部。另外，容易得出 f 是连续的，由 Brouwer 不动点定理可知，存在一个 P 点使得 P=f(P) ，这个 P 点所对应的 Pa 、 Pb 、 Pc 、 Pd 显然就是一个菱形的四个顶点。
沙发
有证明凹多边形的方法么
我觉得你应该多写点算法方面的！纯数学的没几个人愿意看
LS的，这可不一定
最近的几篇好短啊
我对数学的兴趣可以说完全是由这个BLOG激发的
持续期待。。。
哈哈，我猜对了。
对于凹四边形，如果条件弱化为“菱形的四个顶点分别在四条边上”(允许菱形的一部分在四边形外)，则是容易的。
先把四个中点连接起来，便得到了一个平行四边形，然后向凹四边形其中的两个顶点移动，平行四边形便可变形为菱形。
至于超过四边的凹多边形，选取其中的4个边就可以了，有C(n,4)种选法，我想至少有一种菱形的顶点不必落在边的延长线上。
凸多边形一定会有内接圆，圆内必可以做出菱形……
回楼上，你这个想法没有动脑子……或者是我弱了，您解释下，我觉得你的命题和原命题不等价
恩 好像是这样！
第一种证法真是太巧妙了
什么天才都有
哇塞，居然是沙发？留个名