玩转内接多边形（一）：任意多边形内均存在内接正三角形

这本电子书的第五章非常牛 B ，里面讲到了一系列与多边形的内接图形有关的定理及其证明。有意思的是，同样是研究多边形的内接图形，当具体的研究对象不同时，证明手段也各有各的精彩，并且十分难得的是，这些证明都极具欣赏价值。读完这些巧妙的证明后，我迫不及待地想与大家分享。这里我们先来热热身，看一看最简单的情况：一个多边形内是否总能内接一个等边三角形。

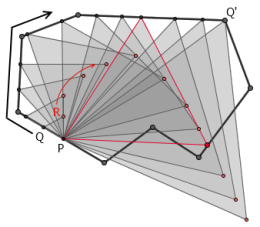
答案是肯定的，任意一个多边形内总存在一个内接等边三角形。一个非常直观的证明是，令 P 为多边形边界上的一点， Q 点为多边形上的一个动点。以 PQ 为边作等边三角形，把这个三角形的第三点记作 R 。当 Q 离 P 点充分近的时候， R 显然在多边形内部；当 Q 点运动到离 P 点最远处 Q’ 时，多边形内的任意一点到 P 的距离都比 PQ’ 小，因此此时 R 点只可能在多边形外。但 R 的运动轨迹显然是连续的，因此在运动过程中它一定经过了多边形的边界。此时，我们就找到了多边形边界上的三个点 P 、 Q 、 R ，它们组成了一个等边三角形。

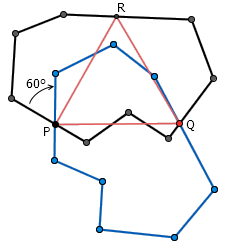
另一个漂亮的证明如上图所示。令 P 为多边形某条边上的一点，将整个多边形顺时针绕 P 点旋转 60 度。显然， P 点所在的线段经过旋转后，有一部分将落在原多边形内，有一部分将落在原多边形外。因此，旋转后的多边形必然与原多边形的边界有其它交点，否则它的边不可能形成一条封闭的回路。不妨设另一交点为 Q ，再把 Q 点绕 P 逆时针旋转 60 度后得到的点记作 R 点。那么显然 R 点在原多边形上，并且 △PQR 是一个等边三角形。

注：这一系列证明中有很多是不完整的，许多看似显然的细节实际上有待进一步去证明。但是，这仍然不影响我们去欣赏这些优雅的证明（尤其是它们的思路）。

16 条评论