如何构造一个平滑的最大值函数

    在处理最优化问题时，我们常常通过分析导函数来寻找极值点，因此往往希望目标函数是可导的；但在很多实际问题中，目标函数里经常带有取最大值函数，它的存在将破坏函数的可导性。一个有趣的问题由此产生：能否设计一个平滑的二元函数 f(x,y) ，它的效果近似于 max(x,y) ，足以用来代替最大值函数？在设计这样的函数时，下面这些条件需要尽可能满足：

   · 函数简洁而美观
   · 可以调整函数的“平滑度”
   · 可以很方便地扩展到多个变量


    我在这里发现了一个非常漂亮的构造： ln(exp(x) + exp(y)) 。由于 x 和 y 都在指数位置上，因此它们的差距将会放得很大。比方说， 3 和 8 这两个数虽然相隔不远，但 e^3≈20.0855 ， e^8≈2980.96 ，两个幂差了几个数量级。因此，把 e^3 加到 e^8 上，几乎不会改变 e^8 的大小。对 e^3+e^8 取对数的结果和直接对 e^8 取对数的结果相差不多。事实上， ln(exp(3) + exp(8))≈8.00672 ，非常逼近最大值函数的结果。

 
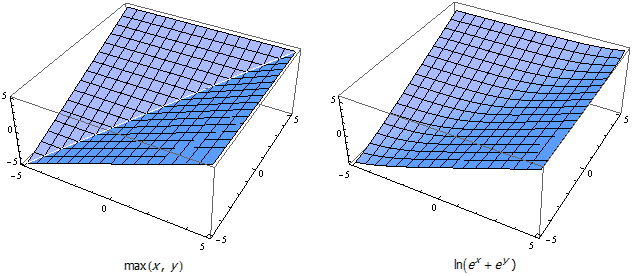
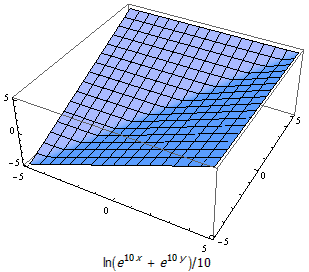
    这个函数有很多好处。首先，它看上去非常漂亮，并且很容易参与到其它运算中。其次，它可以非常方便地扩展到 n 个变量的情况，即 ln(exp(x_1) + exp(x_2) + … + exp(x_n)) 。另外，这个函数的精确程度是可以控制的。显然，由于指数函数越到后面变化幅度越大，因此这个函数对尺度较大的变量来说会变得更加精确。如果把 3 和 8 变成 30 和 80 ，函数结果可以精确到小数点后 20 多位。因此，我们可以用一个系数 k 来调节变量的尺度，让 x 和 y 同时扩大 k 倍，最后结果再除以 k 。换句话说，把函数重新写成 ln(exp(k·x) + exp(k·y))/k ， k 越大整个函数将越逼近最大值函数， k 越小函数也就变得越平滑。

 
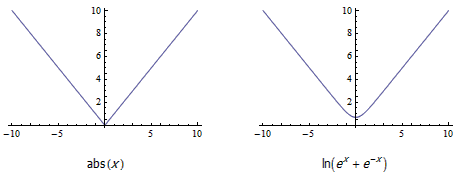
    有了这个函数后，很多本身不可导的函数立即有了可导的近似函数。例如，绝对值函数 abs(x) 其实可以写作 max(x,-x) ，因此可以用可导函数 ln(exp(x) + exp(-x)) 近似代替：

 
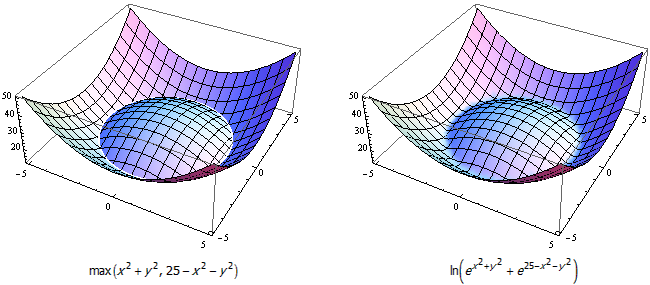
    对于复合函数的情形，用 ln(exp(g(x,y)) + exp(h(x,y))) 代替 max(g(x,y), h(x,y)) 同样能带来很好的效果：

34 条评论

发表评论




Enter Captcha Here :