刚才在这里看到了如题所说的图像，立即想到用 Mathematica 验证一下。我选出了几个个人比较感兴趣的 k ，再用一句话便可输出所有对应 k 的图像：
kArray = {2, 3, 4, 6, 8, 10, 12, 14, 16, 18, 20, 36, 50};
For[i = 1, i <= Length[kArray], i++,
Export["F:\" <> ToString[kArray[[i]]] <> ".png",
ArrayPlot[Table[Boole[Length[Divisors[x*y]] == kArray[[i]]], {x, 1, 400}, {y, 1, 400}],
PixelConstrained -> {1, 1}, Frame -> False]]];
当 k=2 时，由于只有素数才有两个约数，因此所有点都是形如 (p, 1) 或者 (1, p) 的点，其中 p 为某个素数：
当 k=3 时，图像上的点大致成一条斜线，斜线上的点都是形如 (p, p) 的点，其中 p 为某个素数：
当k是更大一些的奇数时，情况类似，因此不再重复了。
当 k=4 时，图像上出现了很多竖直线和水平线，这些直线的位置与素数的平方相对应：
当 k=6 时，逐渐出现了一些乍看之下不好理解的元素：
当 k=8 时，出现了之前不曾见过的情况：图中有一些连续的直线段：
当 k=10 时：
当 k=12 时：
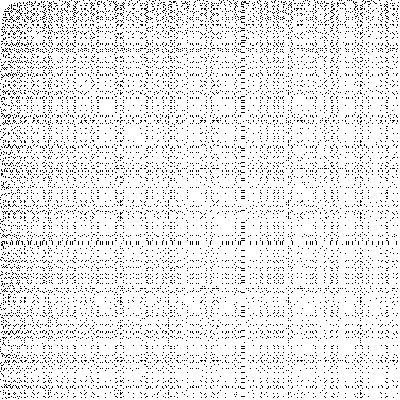
当 k=14 时：
当 k=16 时，更加怪异了：
当 k=18 时：
当 k=20 时：
当 k=36 时：
当 k=50 时：
研究这些图像各种有趣的模式产生的原因，无疑是一个有趣的课题。
sofa
板凳！
这个跟欧拉公式有挺大关系
建议：x、y可以取实数，但xy为正整数，这样的图像更连续一些，不知道是什么结果。
靠前,
有意思
我是“地*”？
崇拜大牛有一段时间了
因数越多点越密？
想问你个问题：无理数根号2，pi都可以用图形表示出来，那e可以吗？
这个跟欧拉公式有挺大关系+1
能不能再试试其它的2^n,说不定更有趣…
真的很有趣啊！！！变成圆的了^^
12楼那个不是圆而是一个双曲线…
实际是对k是xy进行分解后所有质因子次数+1的乘积。之所以偶数图像有趣就是因为这意味着至少xy有一个偶重质因子，这保证了x与y不互质的出现，所以图像就好玩了。
sorry上边写错了，其实图像似乎和xy是否互质没什么关系
Matrix67的Mathematica用的真实登峰造极啊
看了一上午介绍和12345，总算才知道一点。。。
2^n 似乎都有些奇怪得样子。
画成个立体图应该很有意思
把k作为竖坐标绘图
64呢？128呢？256呢？
把 k从小到大的几个图片连结成一个gif~~哈哈 ~
蛮不错！
你有没有发现，把斐波纳吉数列按照n进制排列，取出每个数个位数，另这些个位数排成的数列为a（n)，由（a(n),a(n+1)）组成的图像各不相同。
program feibonaki;
uses graph,crt;
const
x1=52; y1=2;
x2=2; y2=2;
x3=20; y3=8;
color=white;
density=2000;{2<=density<=2000}
timestep=2;{2<=timestep=i then a[n]:=a[n]-i;
if (a[n]=0) and (a[n-1]=1) then over:=true;
n:=n+1;
until over=true;
bar(x1,y1,i+x1,j+y1);
for j:=1 to n do
putpixel(a[j-1]+x1,a[j]+y1,color);
str(n-1,str1);
str(i,str2);
bar(x2,y2,x2+x3+x3,y2+y3+y3);
outtextxy(x2,y2,str2);
outtextxy(x2,y2+y3,str1);
outtextxy(x2,y2+i*y3,str2);
outtextxy(x2+x3,y2+i*y3,str1);
delay(timestep);
end;
readln;
CloseGraph;
end.
漏东西了。
program feibonaki;
uses graph,crt;
const
x1=52; y1=2;
x2=2; y2=2;
x3=20; y3=8;
color=white;
density=2000;{2<=density<=2000}
timestep=2;{2<=timestep=i then a[n]:=a[n]-i;{取个位数}
if (a[n]=0) and (a[n-1]=1) then over:=true;{判断是否已循环}
n:=n+1;
until over=true;
bar(x1,y1,i+x1,j+y1);
for j:=1 to n do
putpixel(a[j-1]+x1,a[j]+y1,color);
str(n-1,str1);
str(i,str2);
bar(x2,y2,x2+x3+x3,y2+y3+y3);
outtextxy(x2,y2,str2);
outtextxy(x2,y2+y3,str1);
outtextxy(x2,y2+i*y3,str2);
outtextxy(x2+x3,y2+i*y3,str1);
delay(timestep);
end;
readln;
CloseGraph;
end.
var
gd,gm:integer;
i,j,n:integer;
a:array[0..42000] of integer;
over:boolean;
str1,str2:string;
begin
gd:=detect; {
gd:=D8bit;
gm:=m640x480;}
InitGraph(gd,gm,”);
Assert(graphResult=grOk);
for i:=2 to density do
begin
over:=false;
a[0]:=0;
a[1]:=1;
n:=2;
repeat
a[n]:=a[n-1]+a[n-2];{斐波纳吉数列生成}
if a[n]>=i then a[n]:=a[n]-i;{取个位数}
for i:=2 to density do
begin
over:=false;
a[0]:=0;
a[1]:=1;
n:=2;
repeat
a[n]:=a[n-1]+a[n-2];{斐波纳吉数列生成}
if a[n]>=i then a[n]:=a[n]-i;{取个位数}
if (a[n]=0) and (a[n-1]=1) then over:=true;{判断是否已循环}
n:=n+1;
until over=true;
bar(x1,y1,i+x1,j+y1);
for j:=1 to n do
putpixel(a[j-1]+x1,a[j]+y1,color);
str(n-1,str1);
str(i,str2);
bar(x2,y2,x2+x3+x3,y2+y3+y3);
outtextxy(x2,y2,str2);
outtextxy(x2,y2+y3,str1);
outtextxy(x2,y2+i*y3,str2);
outtextxy(x2+x3,y2+i*y3,str1);
delay(timestep);
end;
readln;
CloseGraph;
end.
program sushuxy; {本素数xy程序}
uses graph,crt;
const
color=white;
density=800;
display=250;
timestep=10;
clean=false;
colorchange=true;
var {本素数xy程序}
gd,gm:integer;
i,j,k,color1,p:integer;
a:array[0..density,0..density] of integer;
str1,str2:string;
begin {本素数xy程序}
gd:=detect; {
gd:=D8bit;
gm:=m640x480;}
InitGraph(gd,gm,”);
Assert(graphResult=grOk);
p:=(density div 2);
color1:=color;
for i:=1 to density do
begin
str(i,str1);
bar(p,p,p+30,p+10);
outtextxy(p,p,str1);
for j:=1 to density do
begin
for k:=1 to round(sqrt(i*j))-1 do
if (((i*j) mod k)=0) then a[i,j]:=a[i,j]+2;
if ((i*j) mod round(sqrt(i*j))=0) then a[i,j]:=a[i,j]+1;
end;
end;
for k:=1 to display do {本素数xy程序}
begin
if clean then bar(0,0,density,density);
for i:=1 to density do
for j:=1 to density do
begin
if colorchange then color1:=k;
if a[i,j]=k then putpixel(i,j,color1);
end;
str(k,str2);
bar(p,p,p+30,p+10);
outtextxy(p,p,str2);
delay(timestep);
end;
readln;
CloseGraph;
end.
const
x1=52; y1=2;
x2=2; y2=2;
x3=20; y3=8;
color=white;
density=2000;{2<=density<=2000}
timestep=2;{2<=timestep=i then a[n]:=a[n]-i;
if (a[n]=0) and (a[n-1]=1) then over:=true;
n:=n+1;
until over=true;
bar(x1,y1,i+x1,j+y1);
for j:=1 to n do
putpixel(a[j-1]+x1,a[j]+y1,color);
str(n-1,str1);
str(i,str2);