下面分享的是我自己写的三个代码，里面有些题目也是我自己出的。这些代码都是在我的Pascal时代写的，恕不提供C语言了。代码写得并不好，我只是想告诉大家位运算在实战中的应用，包括了搜索和状态压缩DP方面的题目。其实大家可以在网上找到更多用位运算优化的题目，这里整理出一些自己写的代码，只是为了原创系列文章的完整性。这一系列文章到这里就结束了，希望大家能有所收获。
Matrix67原创，转贴请注明出处。
Problem : 费解的开关
题目来源
06年NOIp模拟赛（一） by Matrix67 第四题问题描述
你玩过“拉灯”游戏吗？25盏灯排成一个5×5的方形。每一个灯都有一个开关，游戏者可以改变它的状态。每一步，游戏者可以改变某一个灯的状态。游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字“1”表示一盏开着的灯，用数字“0”表示关着的灯。下面这种状态10111
01101
10111
10000
11011在改变了最左上角的灯的状态后将变成：
01111
11101
10111
10000
11011再改变它正中间的灯后状态将变成：
01111
11001
11001
10100
11011给定一些游戏的初始状态，编写程序判断游戏者是否可能在6步以内使所有的灯都变亮。
输入格式
第一行有一个正整数n，代表数据中共有n个待解决的游戏初始状态。
以下若干行数据分为n组，每组数据有5行，每行5个字符。每组数据描述了一个游戏的初始状态。各组数据间用一个空行分隔。
对于30%的数据，n<=5；
对于100%的数据，n<=500。输出格式
输出数据一共有n行，每行有一个小于等于6的整数，它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态，若6步以内无法使所有灯变亮，请输出“-1”。样例输入
3
00111
01011
10001
11010
1110011101
11101
11110
11111
1111101111
11111
11111
11111
11111样例输出
3
2
-1
程序代码const
BigPrime=3214567;
MaxStep=6;
type
pointer=^rec;
rec=record
v:longint;
step:integer;
next:pointer;
end;
var
total:longint;
hash:array[0..BigPrime-1]of pointer;
q:array[1..400000]of rec;
function update(a:longint;p:integer):longint;
begin
a:=a xor (1 shl p);
if p mod 5<>0 then a:=a xor (1 shl (p-1));
if (p+1) mod 5<>0 then a:=a xor (1 shl (p+1));
if p<20 then a:=a xor (1 shl (p+5));
if p>4 then a:=a xor (1 shl (p-5));
exit(a);
end;
function find(a:longint;step:integer):boolean;
var
now:pointer;
begin
now:=hash[a mod BigPrime];
while now<>nil do
begin
if now^.v=a then exit(true);
now:=now^.next;
end;
new(now);
now^.v:=a;
now^.step:=step;
now^.next:=hash[a mod BigPrime];
hash[a mod BigPrime]:=now;
total:=total+1;
exit(false);
end;
procedure solve;
var
p:integer;
close:longint=0;
open:longint=1;
begin
find(1 shl 25-1,0);
q[1].v:=1 shl 25-1;
q[1].step:=0;
repeat
inc(close);
for p:=0 to 24 do
if not find(update(q[close].v,p),q[close].step+1) and (q[close].step+1<MaxStep) then
begin
open:=open+1;
q[open].v:=update(q[close].v,p);
q[open].step:=q[close].step+1;
end;
until close>=open;
end;
procedure print(a:longint);
var
now:pointer;
begin
now:=hash[a mod BigPrime];
while now<>nil do
begin
if now^.v=a then
begin
writeln(now^.step);
exit;
end;
now:=now^.next;
end;
writeln(-1);
end;
procedure main;
var
ch:char;
i,j,n:integer;
t:longint;
begin
readln(n);
for i:=1 to n do
begin
t:=0;
for j:=1 to 25 do
begin
read(ch);
t:=t*2+ord(ch)-48;
if j mod 5=0 then readln;
end;
print(t);
if i<n then readln;
end;
end;
begin
solve;
main;
end.
======================= 性感的分割线 =======================
Problem : garden / 和MM逛花园
题目来源
07年Matrix67生日邀请赛第四题问题描述
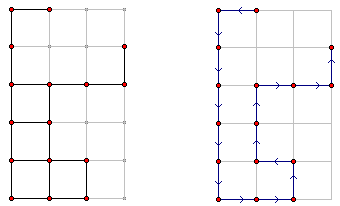
花园设计强调，简单就是美。Matrix67常去的花园有着非常简单的布局：花园的所有景点的位置都是“对齐”了的，这些景点可以看作是平面坐标上的格点。相邻的景点之间有小路相连，这些小路全部平行于坐标轴。景点和小路组成了一个“不完整的网格”。
一个典型的花园布局如左图所示。花园布局在6行4列的网格上，花园的16个景点的位置用红色标注在了图中。黑色线条表示景点间的小路，其余灰色部分实际并不存在。
Matrix67 的生日那天，他要带着他的MM在花园里游玩。Matrix67不会带MM两次经过同一个景点，因此每个景点最多被游览一次。他和他
sofa!
拜托，程序加点注释或者算法介绍好不好？
这么长的程序，要人家一个一个看很累欸。
回复：每个函数是干啥的看函数名就知道了
有时间我再来加注释吧
M67的代码写法和我的好像啊。。。
可是为什么感觉我的没这么好看呢 。
有些别扭
最后貌似少了两行什么东东 ~
[eek]原来在前面……
文章太长……
看到后面就忘记前几行了
Andriy MM..
学P的代码大致这个写法…
回复：支持！pascal最普遍、最准确的写法就是这样，写出来很好看；而写C代码不同人有不同习惯（比如{的位置），而且改代码风格改过去改过来老是觉得不好看
读读这句话
如果改变其中一盏灯则它本身以及它下面一格的和下面两格的以及左下一格的和右下一格的都会变
BigPrime=3214567;
– -弱弱的问一下…
这个是怎么得额来的哦？
分割线让人无语啊
我来补充一下题解：
费解的开关
首先可以把25个灯表示成25位二进制，然后再转成十进制。灯的转换可以用“要转换的灯 xor 1”来做，因为xor 1就是01相反。本题搜索的巧妙之处就是从最终状态（全1）反向BFS，搜6步，然后将状态用hash存下。以后输出直接拿出来用就可以了，如果在hash表中找不到就输出-1。
注意：输入全1输出0。
和MM逛花园
直接枚举所有初始情况的DFS，用位运算把每行（已经走过的点为1）的状态存下来，用来判断点是否已经走过。
玉米地
把地图存在map中。
先来看单单一行能哪些状态是可行的，不考虑不能种的地，我们需要状态中不存在连续的1，用程序中的impossible函数来判断。可行的状态存在st数组中。
然后地推，f[I,j]表示到第i行，第i行状态为j的方案数，枚举第i-1行的状态k。要满足两个条件：
1：j和map[i]不能冲突，也就是不能有不能种的地。
2:k和map[i-1]不能冲突。
3：j和k不能冲突。
那么f[I,j]:=f[I,j]+f[I-1,k]。
orz
第三题的impossible是不是。。
直接exit(not(a xor (a shr 1))=0)就行了吧。。
错了。。楼上xor改为and。。
Orz Martrix67 神牛…
明天就NOIP2009了
orz 神牛 后天noip2010…..
太好了，很受用
钦佩之至，这四篇文章我要仔细研究下
想到一个很邪恶的事：第一题可以用位运算打表。。。
逛花园的标程好像不对。
我不得不说第一题Matrix67大牛的做法太复杂⋯⋯貌似有规律改进算法
不大习惯pascal，不知道学pascal的看C++怎样
太好了，很受用
文章不完整，到第二个例子就被截断了？什么情况？？
一样
//·¸ÁË´í£¬µÚÒ»¸ösolve()µ÷ÓÃû¼ÓÀ¨ºÅ£¬µÚ¶þ¸ö (1<<25)-1 û¼ÓÀ¨ºÅ
#include
#include
using namespace std;
const int BigPrime=3214567;
const int MaxStep=6;
struct recNode{
long long v;
int step ;
long long next ;
};
long long tot=0,head=0,tail=0;
long long hash[BigPrime];//ÅжÏÕâ¸ö״̬ÓÐû³öÏÖ
recNode rec[BigPrime];
recNode q[BigPrime];
char ch;
int n;
long long t;
long long update(long long a,int p )//25¸öλÖÃa ¸Ä±äpµÄλÖÃ
{
a=a ^ (1<<p);//pµ±Ç°Î»Öøü¸Ä
if (p % 5!=0) a=a ^ (1 << (p-1));//p×ó²àλÖøü¸Ä ²»ÊÇ×î×ó±ß
if ((p+1) % 5!=0 )a=a ^ (1<<(p+1));//pÓÒ²àλÖøü¸Ä ²»ÊÇ×îÓÒ±ß
if (p<20)a=a ^ (1 <4) a=a ^ (1 <0)
{
if (rec[now].v==a)return true;
now=rec[now].next;
}
tot++;
rec[tot].v=a;
rec[tot].step=step;
rec[tot].next= hash[a%BigPrime];//²»ÊÇnow ÓпÉÄÜÏòºóÕÒÁËÏàͬhashÖµµÃ
hash[a%BigPrime]=tot;
return false;//ÔÀ´Ã»ÓУ¬ÏÖÔÚн¨ÁË
}
void solve()
{
find((1<<25)-1,0);//ÏȸøÈ«1 ¸³Öµ0²½ ²¢·ÅÈëÊý×éÖÐ
tail++;
q[tail].v=(1<<25)-1;
q[tail].step=0;
//°Ñ×îÖÕÈ«1״̬ ÿ´Î·25ÖÖ¿ÉÄÜ Èë¶Ó£¬ÏòÉÏ×ß6²½
while(head<tail)
{
head++;//µÚÒ»¸ö³ö¶Ó
for(int p=0;p<25;p++)
{
long long t=update(q[head].v,p);//¸üжÓÊ×µÚp¸öλÖà ºó״̬
int step=q[head].step;
//Èç¹û ÔÀ´Ã»ÓÐÕâ¸ö״̬ ,ÇÒÔÚ6²½Ö®ÄÚ£¬ÔòÈë¶Ó
if(find(t,step+1)==false && step+10)
{
if(rec[now].v==a)
{
printf(“%d\n”,rec[now].step);
return;
}
now=rec[now].next;
}
printf(“-1\n”);//×îÖÕûÕÒµ½ 6²½Ö®ÄÚûÕâ¸ö״̬
}
int main()
{
solve();//Ô¤ÏÈ´¦Àí
cout<<"´¦ÀíÍê±Ï\n";
//for(int i=1;i<5;i++)cout<<rec[i].v<<" "<<rec[i].step<<endl;
scanf("%d",&n);
getchar();//Ïûµô»Ø³µ
for(int i=0;i<n;i++)//n×éÊý
{
t=0;
for(int j=1;j<=25;j++)
{
ch=getchar();
t=(long long)(t*2+(ch-'0'));
if(j%5==0)getchar();//¶Á¸ö»Ø³µ
}
//cout<<t<<endl;
prt(t);
if(i<n)getchar();//¶à×éÊýÖ®¼äÓиö¿ÕÐÐ
}
//getchar();
return 0;
}
/*
ÑùÀýÊäÈë
3
00111
01011
10001
11010
11100
11101
11101
11110
11111
11111
01111
11111
11111
11111
11111
ÑùÀýÊä³ö
3
2
-1
*/