今天我们来看两个稍微复杂一点的例子。

n皇后问题位运算版
    n皇后问题是啥我就不说了吧，学编程的肯定都见过。下面的十多行代码是n皇后问题的一个高效位运算程序，看到过的人都夸它牛。初始时，upperlim:=(1 shl n)-1。主程序调用test(0,0,0)后sum的值就是n皇后总的解数。拿这个去交USACO，0.3s，暴爽。
procedure test(row,ld,rd:longint);
var
      pos,p:longint;
begin

{ 1}  if row<>upperlim then
{ 2}  begin
{ 3}     pos:=upperlim and not (row or ld or rd);
{ 4}     while pos<>0 do
{ 5}     begin
{ 6}        p:=pos and -pos;
{ 7}        pos:=pos-p;
{ 8}        test(row+p,(ld+p)shl 1,(rd+p)shr 1);
{ 9}     end;
{10}  end
{11}  else inc(sum);

end;
    乍一看似乎完全摸不着头脑，实际上整个程序是非常容易理解的。这里还是建议大家自己单步运行一探究竟，实在没研究出来再看下面的解说。

  
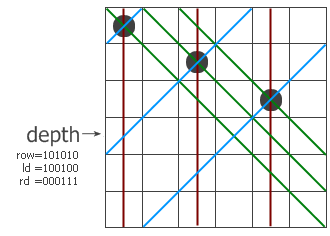
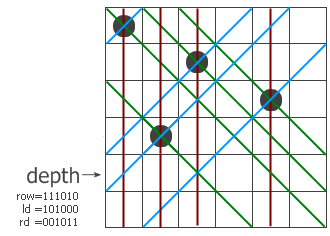
    和普通算法一样，这是一个递归过程，程序一行一行地寻找可以放皇后的地方。过程带三个参数，row、ld和rd，分别表示在纵列和两个对角线方向的限制条件下这一行的哪些地方不能放。我们以6x6的棋盘为例，看看程序是怎么工作的。假设现在已经递归到第四层，前三层放的子已经标在左图上了。红色、蓝色和绿色的线分别表示三个方向上有冲突的位置，位于该行上的冲突位置就用row、ld和rd中的1来表示。把它们三个并起来，得到该行所有的禁位，取反后就得到所有可以放的位置（用pos来表示）。前面说过-a相当于not a + 1，这里的代码第6行就相当于pos and (not pos + 1)，其结果是取出最右边的那个1。这样，p就表示该行的某个可以放子的位置，把它从pos中移除并递归调用test过程。注意递归调用时三个参数的变化，每个参数都加上了一个禁位，但两个对角线方向的禁位对下一行的影响需要平移一位。最后，如果递归到某个时候发现row=111111了，说明六个皇后全放进去了，此时程序从第1行跳到第11行，找到的解的个数加一。

    ~~~~====~~~~=====   华丽的分割线   =====~~~~====~~~~

Gray码
    假如我有4个潜在的GF，我需要决定最终到底和谁在一起。一个简单的办法就是，依次和每个MM交往一段时间，最后选择给我带来的“满意度”最大的MM。但看了dd牛的理论后，事情开始变得复杂了：我可以选择和多个MM在一起。这样，需要考核的状态变成了2^4=16种（当然包括0000这一状态，因为我有可能是玻璃）。现在的问题就是，我应该用什么顺序来遍历这16种状态呢？
    传统的做法是，用二进制数的顺序来遍历所有可能的组合。也就是说，我需要以0000->0001->0010->0011->0100->...->1111这样的顺序对每种状态进行测试。这个顺序很不科学，很多时候状态的转移都很耗时。比如从0111到1000时我需要暂时甩掉当前所有的3个MM，然后去把第4个MM。同时改变所有MM与我的关系是一件何等巨大的工程啊。因此，我希望知道，是否有一种方法可以使得，从没有MM这一状态出发，每次只改变我和一个MM的关系（追或者甩），15次操作后恰好遍历完所有可能的组合（最终状态不一定是1111）。大家自己先试一试看行不行。
    解决这个问题的方法很巧妙。我们来说明，假如我们已经知道了n=2时的合法遍历顺序，我们如何得到n=3的遍历顺序。显然，n=2的遍历顺序如下：

00
01
11
10

    你可能已经想到了如何把上面的遍历顺序扩展到n=3的情况。n=3时一共有8种状态，其中前面4个把n=2的遍历顺序照搬下来，然后把它们对称翻折下去并在最前面加上1作为后面4个状态：

000
001
011
010  ↑
--------
110  ↓
111
101
100

    用这种方法得到的遍历顺序显然符合要求。首先，上面8个状态恰好是n=3时的所有8种组合，因为它们是在n=2的全部四种组合的基础上考虑选不选第3个元素所得到的。然后我们看到，后面一半的状态应该和前面一半一样满足“相邻状态间仅一位不同”的限制，而“镜面”处则是最前面那一位数不同。再次翻折三阶遍历顺序，我们就得到了刚才的问题的答案：

0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000

    这种遍历顺序作为一种编码方式存在，叫做Gray码（写个中文让蜘蛛来抓：格雷码）。它的应用范围很广。比如，n阶的Gray码相当于在n维立方体上的Hamilton回路，因为沿着立方体上的边走一步，n维坐标中只会有一个值改变。再比如，Gray码和Hanoi塔问题等价。Gray码改变的是第几个数，Hanoi塔就该移动哪个盘子。比如，3阶的Gray码每次改变的元素所在位置依次为1-2-1-3-1-2-1，这正好是3阶Hanoi塔每次移动盘子编号。如果我们可以快速求出Gray码的第n个数是多少，我们就可以输出任意步数后Hanoi塔的移动步骤。现在我告诉你，Gray码的第n个数（从0算起）是n xor (n shr 1)，你能想出来这是为什么吗？先自己想想吧。

    下面我们把二进制数和Gray码都写在下面，可以看到左边的数异或自身右移的结果就等于右边的数。

二进制数   Gray码
   000       000
   001       001
   010       011
   011       010
   100       110
   101       111
   110       101
   111       100

    从二进制数的角度看，“镜像”位置上的数即是对原数进行not运算后的结果。比如，第3个数010和倒数第3个数101的每一位都正好相反。假设这两个数分别为x和y，那么x xor (x shr 1)和y xor (y shr 1)的结果只有一点不同：后者的首位是1，前者的首位是0。而这正好是Gray码的生成方法。这就说明了，Gray码的第n个数确实是n xor (n shr 1)。

    今年四月份mashuo给我看了这道题，是二维意义上的Gray码。题目大意是说，把0到2^(n+m)-1的数写成2^n * 2^m的矩阵，使得位置相邻两数的二进制表示只有一位之差。答案其实很简单，所有数都是由m位的Gray码和n位Gray码拼接而成，需要用左移操作和or运算完成。完整的代码如下：
var
   x,y,m,n,u:longint;
begin
   readln(m,n);
   for x:=0 to 1 shl m-1 do begin
      u:=(x xor (x shr 1)) shl n; //输出数的左边是一个m位的Gray码
      for y:=0 to 1 shl n-1 do
         write(u or (y xor (y shr 1)),' '); //并上一个n位Gray码
      writeln;
   end;
end.

Matrix67原创
转贴请注明出处