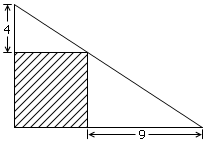
今天在某小学数学竞赛真题上看到了这么一个问题：图中阴影部分是一个正方形，求它的边长。当然，题目本身并不难，大家一看就知道答案；问题的关键在于，这个问题是一道小学竞赛题，这意味着这个题目一定有一个异常巧妙的傻瓜解。这个解法不用相似形，不用列方程，事实上几乎什么都不用，只需要用到最基本最显然的正方形长方形的性质。你能想到这个解法吗？
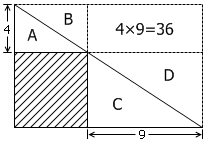
反正我是没想到，然后翻了翻答案，顿时感觉小学奥数思维之妙：把图形补充为一个长方形，则两个大的直角三角形面积相同，另外还有A的面积与B的面积相同，C的面积与D的面积相同。于是我们得到，阴影部分与右上角的那个小长方形面积相同，而后者的面积应该是36。这就是说，正方形的边长应该等于6。
我不由得开始思考，中学数学的学习真的禁锢了我们的思维吗？
偶尔沙发一次
嗯，的确巧妙，反正我是没想出来……
为什么面积等于底*高？两个线段相乘是什么意思？
哈哈 想出来了
不过你的提示已经提到长方形了哦~
我一般都是这么做的填空题
为什么面积等于底*高？因为图形的面积等于该图形所含单位正方形的个数。
中学生应该读《几何原本》，至少中学数学老师应该读。
不用吧，左上角和右下角的三角形是相似的（汗，都不知道怎么表达了。）
所以
4/边长=边长/9
边长=6
我竟然一看题目就脑海中补全了长方形，直觉告诉我把4*9乘起来，然后发现6是整数，bingo！
为什么面积等于底*高？因为图形的面积等于该图形所含单位正方形的个数。
如果是有理数好理解 ，但是无理数呢，是什么意思呢 ，不好理解
巧妙
primary education will blow your mind!
错了，方程和代数是更本质的东西，这是需要普及的数学思想，而补全挖空这样一些技巧，才是数学爱好者需要掌握的各种捷径。
如果正方形变长为6的话 那么 为什么√（4^2+6^2) + √(6^2+9^2) 与 √(10^2+15^2) 不相等呢？
小学奥数吗？这个方向不错
一直认为，奥数一类的东西，应该是用来拓宽思维的，而不是高中奥数一样为了解怪题。那没有意义
希望我们的下一代不要被前人所束缚。。
的确是很巧妙的做法
用这张图来证明sqrt(52)+sqrt(115)=sqrt(315)就强了
我算数太差了
学了方程后感觉自己变笨了，什么都依赖方程。
小学奥数很锻炼思维，为后来搞计算机奥赛提供了很多思路。
中学奥数就没意思了，就是超前学习，解怪题难题，没意思，学到了那一步自然会解，小学奥数完全不一样~
拓宽思路，对思维的训练很有帮助~
方程N年后 小学方法都忘完了。。。
实际上从小学高年级起就一直方程
otter says :
如果正方形变长为6的话 那么 为什么√（4^2+6^2) + √(6^2+9^2) 与 √(10^2+15^2) 不相等呢？
——-
你的后一个式子中的10和15是什么东西？
斜边不是两直角边之和（4＋6＝10，6＋9＝15），而是直角边平方之和再开方。。
要想到补成矩形还是蛮难的！
我觉得是：中学数学的学习真的禁锢了我们的思维。
14楼的问题怎么回答？晕了……
明白了，被17楼搞晕了，17楼是错误的，不知道115和315从何而来。14楼是相等的。
同意 中学禁锢论
额，的确很巧妙~~~怎么都没想到。。。思维呀，要发散点！！！
想到一半没想出来，结果忍不住看了答案。
我发现LS有个没仔细看文章就回复的人……就是那个Eric
(A=B)AND(C=D) THEN (S=S)
猛烈拥护ls && lss T-T
12a讲得挺对的，沉溺于技巧往往会忽略数学的本质。
膜拜最后一句@@@@@@@@
说的太好了********
没想出来就是了
现在越来越笨了
看这题想起了一个美国数学家，玩图形很厉害的那个,明天上图馆掘书去…
用学校里的话说是“技巧性很强”，也就是普遍性很差，会了这一题，对解其他的题不能照搬方法，说得直一些就是“怪癖、另类”。
这道题的补全还算是比较通用的方法呢，其实中学题目里也有许多需要补全或者辅助线不是吗？真正的数学高手就是这方面的思维厉害，只有靠多想多实践，没法总结编程的，这一点计算机真的要过100年还不一定能学会呢
太神奇了..前天才被问到这个题目 也是复原成一个矩形 但是那个正方形的条件不是必要的,,,很多余啊~~~
一看就知道~因为以前见过类似的东西~~小学总爱搞这种小聪明小技巧，sigh
不过话说这题的技巧算是还有一定的普遍性来着
这个问题还可以这么解：
2 * a^2 = (4+a)(9+a) – 4a – 9a
正方形的面积 = 大三角形的面积 – 两个小三角形的面积
化简一下上式，直接得到 a^2 = 36
貌似这么解也不用相似形
40L又一个回复不看原文的
“这个解法不用相似形，不用列方程”
你那个方法是个人就能想到，不用写出来
我真的是没想到，脑子笨成猪脑子了！
这个，你的解法太复杂了吧
两个三角形的角相等，所以边长比相等，4:n=n:9
43L又见不看原文者
想到了据说是 slashdot 上故事：数学家冒充水管工，然后用微积分证明圆面积公式……
…ORZ…我是想到了.
牛X！Orz一下
的确是个奇妙的方法，但是我觉得还是解方程更快一些……
小学时做这题时好像我就想到了……
模式毁灭创造性
很好。
Many people will know of me from the uncannily accurate readings I gave listeners to The Third Eye radio show, both by phone and email.
You may also have read about me in CHAT, It’s Fate, The Daily Express, Psychic News, The East Anglian Times and other newspapers that have written about my work.
I am here to help you in whatever way I can. Having given psychic readings for many years, practice makes perfect and I have earned a reputation for considerable accuracy.
You can consult me on any issue that would like some insight, guidance or advice. I don’t judge, so you can be frank and honest about any problem and in complete confidence.
It may be to do with relationships, finances, career prospects, house moves, job hunting, family problems…or for dealing with your problems for the here and now but usually I’ll cover at least the next three months.
Whatever your problem, just outline it to me and send me three questions and I will look in depth at your situation. I do like my readings to be positive and for every problem there is a solution.
Whatever your problem, I’ve probably been through it myself which is why I don’t judge and why I have empathy and care for my clients. Sometimes we all need help and guidance.
I can also explore your spirit guides and who they are if ist something that is puzzling you on your spiritual path.
I can also do workshops or group readings dependent on area and group numbers.
You will find me friendly and approachable and I always try to keep a sense of humour on life.
Also if you feel you have spirit activity in your home I am happy to come and have a look for you. I am experienced in this and have done this many times before successfully.
这是咋回事？
建议把rss改为不要显示全文。。。否则我经常在不经意间看到答案
我有另一个不用方程和相似的办法……
过大三角形的直角顶点作正方形的对角线，分成两个等高的三角形……
然后……面积法……
呃……想晕了……
好像还是方程……
使劲想，死想…唉…想出来了~~
我连方程都没列出一个简单的。好久没这么动过脑子了。
这么简单的方法还真没想出来。。
耶，我竟然想到了！
禁锢禁锢禁锢禁锢禁锢禁锢禁锢禁锢禁锢禁锢禁锢
我居然想到把它补充成一个长方形了呃……
太有才了
被雷到了。。。。
这个题。。。华罗庚也难做- –
像这样的想法，倒是很有可能出现在“劳动人民”的脑海中，这是智慧，不是知识。
当然，利用什么勾股定理啊，三角形相似这类“智慧结晶”也可以解决这类问题，但是始终觉得不如这种“天然”的解法来得美。
我一生就在这四角的围墙（《故乡》）里度过啦……
惯性思维和创新思维的差别～～～
所以有了一些课程就是关于创新思维的～～
不过，再创新，也是得有基础才行的～
强！
我刚开始也觉得应该用相似做
没想到……
简单的方程也可以求解。设正方形的边长为X，则可知，A+C+X的平方的面积=整个大三角形的面积。即：(4+X)*(9+X)/2=4X/2+X2+9X/2 求解X=6
我觉得补完长方形根本就是多此一举，想象不到的还要画个图。这道题的王道就是相似三角形：左上角和右下角三角形相似，方程都不用列就能知道是根号36了。
不赞同你的观点。建议您读一下龚昇的《微积分五讲》。代数、方程要比这种所谓的技巧更接近数学的本质。
不知道怎么用trackback…转到sina了。
试试头像
开平方没有超纲？
How can I know C=C?
看了您两篇博客，发现自己爱上数学了！！
在看到提示有长方形的情况下，想到了，呵呵
我就没明白，两个三角形相当就能推断，正方形和长方形相等？
先算了一下结果是6，于是不知不觉就猜到了方法。
先算了一下结果是6，于是就猜到了下一步。
没想到
说实话，我小学搞竞赛时在书上看过这道习题，当时就想到补三角形的方法了……
面积为什么等于长x宽?好问题。
这全乎是由面积的定义导出的：覆盖所给图形所需的单位正方形的数目即为面积。对长宽皆为整数的长方形，面积等于长乘宽再显然不过了；有理数边长情况下，可以在用单位正方形铺满后进而用百分之一单位正方形铺，再用万分之一，等等。
无理数呢?显然不可能铺得满，但我们可以在给定最小分度的基础上给出有理近似解。取其极限，即可得面积了。
呵呵 不知道耶！求解！
我也想到了······
看来初中两年的教育还没完全禁锢我的思维······
我怎么觉得变相利用了相似或者全等？如果干掉那个正方形，让俩三角形等边接在一起不就是一个直角三角形求斜边高的问题- -。。。
好吧我承认确实么想到。。。
这道题的王道就是相似三角形：左上角和右下角三角形相似，方程都不用列就能知道是根号36了。
当年在四年级的时候才去学奥数，当时做小学三年级的奥数就彻底服了。真乃奇思妙想，妙哉！