2009-07-17 0:01| 
22 Comments | 本文内容遵从勾股定理有上百种证明，但其实它们都大同小异——无非是构造一组三角形和正方形并进行一系列变换。今天我看到了一个用圆面积来解释勾股定理的办法，颇有一些新意。
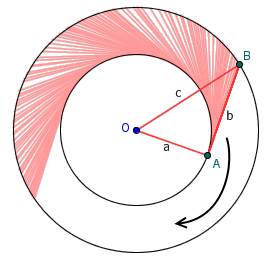
考虑直角三角形OAB绕着一个锐角顶点O旋转一周。顶点A的轨迹是一个半径为a的圆，顶点B的轨迹是一个半径为c的圆。那么，线段AB扫过的区域（一个圆环）的面积就应该是大圆面积减去小圆面积，即π(c^2-a^2)。如果我们能够有一种办法说明，线段AB扫过的面积正好是πb^2，我们就相当于得到了勾股定理的另一个证明。
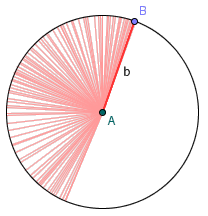
利用微积分或许可以说明这一点，但这里有一个不算严格证明，但却非常直观有趣的想法。考虑线段AB扫过环形区域的过程，它事实上是由平移和旋转两部分叠加构成的——首先沿着圆的切线方向（即BA的方向）平移充分小的距离，然后旋转一个充分小的角度。但很显然，线段沿着自身的方向平移是不会产生面积的，因此线段AB实际扫过的面积就是它绕A点旋转一周的面积，即一个半径为b的圆。从图上看来这一点似乎很显然——上下两个图之间的粉色线条有“一一对应”的关系。这虽然不严密，却是一个很有意思的想法。
来源：http://www.cut-the-knot.org/Curriculum/Geometry/PythFromRing.shtml
沙发，小时候自己也想了若干种证明法，就是无法得知是否与前人的雷同。
坐板凳~ Google Reader 更新还是慢了...
牛～
不严密哎，真的怎么都感觉不严密哎……这咋好一一对应呢？
不严密。从直观上看，如果不是直角三角形，比如说比直角略大一点，那么上面的分析似乎仍然成立，但事实上不是这样。
我也是从reader上来的, 把A所在的圆收缩到一个点上,然后就变成了下图.
其实有点问题。如果一开始不是直角三角形，难道也会得到a^2+b^2=c^2吗。
只是个想法
是不行啊。。如果∠OAB是钝角仍然能得到一样的结论。。
不是直角三角形,线段的“平移”方向就不是在与线段平行的方向了。。。。
我记得我小学时候一年的奥数题就有这个
对于一般的三角形,把线段“平移”对面积的影响就是余弦定理中－2absinC的那一项吧。
对于一般的三角形,线段的“平移”对面积增加的量就对应于余弦定理中-2absinC吧。。
楼上说得对。那这个证明的问题就只在这个“一一对应”不严密上了。我再查查相关资料吧。
让圆环域和圆域中的点按原图的意思,建立起点到点的双射函数,用双重积分换元法,把缩放因子求出为1即可.要严格还是微积分.
呵呵....好特别的证法..
很好很强大的证明
这个证法的逆推不是常用嘛...
太强悍了。。。………………
但是。推算圆的面积需要勾股定理么？
直角三角型的话AB线段的旋转角就和OA线段的旋转角相等～
取某个特定时候的OA线段，之后它转过360,AB也相应的转了360，一一对应～
但不是直角三角形的话，AB线段的旋转角就和OA线段的旋转角不相等！
然后就不知道怎么办了～～～～～
求神牛解决～
AB 和OA 始终是垂直的，因此在OA 的切线的方向上不产生面积，只有旋转产生的面积，相当的合理
直接 微积分搞定他......
[[0-2pie]](1/2sinA*b^2) == pieb^2 == piec^2-piea^2