网友来信：另类线段等分法与距离平方和问题的扩展

    在介绍尺规作图等分圆面积时，我提到了利用尺规作图将线段AB任意等分的问题。在初中课本上，这个问题的标准做法如下：

 
 
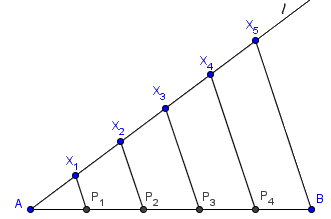
  1. 过A点向另一方向做射线l；
  2. 从A点开始，用圆规在射线l上截取n个等距的点X1, X2, …, Xn；
  3. 连接Xn和B；
  4. 分别过X1, X2, …, Xn-1作直线平行于XnB。

    那么，这些平行线与AB的交点即为AB的n等分点。


    不过，这并不是等分给定线段的唯一做法。在讲解尺规作图时，Wikipedia上给出了一种另类的线段三等分做法：

 
 
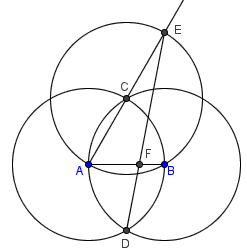
  1. 以AB为半径，分别以A、B为圆心作圆，两圆交于C、D；
  2. 以C为圆心，AC为半径作圆；
  3. 延长AC与圆C交于E；
  4. 连接DE与线段AB交于F。

    则点F就是AB的三等分点。

    网友Liu Qingwei发来邮件说，以前他在某杂志上看到与上面所说方法都不相同的线段n等分法。

 
 
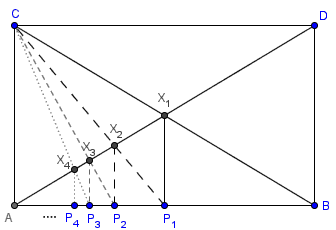
  1. 作出矩形ABDC；
  2. 作出BC和AD的交点，它在AB上的垂足P1就是AB的二等分点；
  3. 作出P1C和AD的交点，它在AB上的垂足P2就是AB的三等分点；
  4. 作出P2C和AD的交点，它在AB上的垂足P3就是AB的四等分点；
   ………

    这样，我们就可以作出线段AB的任意等分点。这个做法的意义在于，我们可以抛弃圆规，只用矩尺便能实现线段的任意等分。

 
   ======================== 我的名字是分割线 ========================
 

    写一个Blog最开心的事情就是能认识各种网友。一位电台DJ留言说他将我前几天写的距离平方和问题进行了推广。注意原问题中内切圆根本不是一个必要的条件，只要是以等边三角形中心为圆心作出的圆，结论都仍然成立。这给了我们很多推广的空间。我们不由得开始猜想，对于一般三角形还有类似的结论吗？可惜的是，用几何画板一画，不但以三角形内心为圆心作圆后原结论不再成立，就连根正苗红的内切圆也失去了原有的性质。为此，我们回到原问题中的证明过程上去。为什么那个证明只对等边三角形有效，对一般三角形就不管用了呢？我们照葫芦画瓢，把一般三角形也放到平面x+y+z=1上，不妨记三个顶点分别在(x1, y1, z1)、(x2, y2, z2)、(x3, y3, z3)，那么所求的距离平方和就应该是x-x1、x-x2、x-x3、y-y1、y-y2、y-y3、z-z1、z-z2、z-z3的平方和。展开后，x^2、y^2和z^2的系数是相同的，它们的和仍然是一个常数。常数项本身就是常数，我们也不必关心它。问题的关键就出在一次项上：式子展开后x、y、z的系数必需相同才能巧用x+y+z=1代换，但这在一般三角形中不一定成立。约去一个比例系数，三个一次项的系数分别为x1+x2+x3、y1+y2+y3、z1+z2+z3。因此，要想让原来的证明仍然适用，必需保证这三组和相等。注意到对每一组(x,y,z)我们都有x+y+z=1，因此9个变量之和应该为3，我们立即可知这三组和其实都等于1。有趣的事情来了，考虑该三角形的质心，(x1+x2+x3)/3、(y1+y2+y3)/3、(z1+z2+z3)/3都等于1/3，而(1/3, 1/3, 1/3)恰好又是平面x+y+z=1上离原点距离最近的位置（也即球x^2+y^2+z^2=r与其相交所成圆的圆心）。因此，我们立即得到这一结论：原题的结论仍然适用于一般三角形及其对应的质心。
    进一步观察我们发现，上述推理过程对于任意多个点都是适用的。对于一个四边形来说，所有12个坐标值的和为4，因此x1+x2+x3+x4、y1+y2+y3+y4、z1+z2+z3+z4均为4/3，其对应的质心坐标依旧为(1/3, 1/3, 1/3)。我们甚至还可以大胆预言，该推理过程甚至能继续适用于更高维的情况……正是这种无穷无尽的推广空间才让数学充满了生机，让思考充满了惊喜和乐趣。

29 条评论

发表评论

2  +  1  =