阴阳图是由两个半圆弧相接组成的曲线把整个圆平分为黑白二色而成。1958年，英国数学家Henry Dudeney在他的著作Amusements in Mathematics中曾经提出了这样一个问题：如何用尺规作出一条同时平分阴阳两部分的曲线？他给出了两种不同的答案。
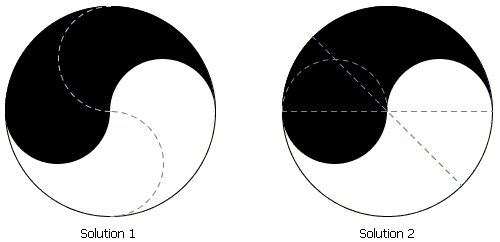
第一种方法是非常完美的，它不但同时平分了阴阳两部分的面积，连分出来的形状也完全相同。另一种办法也非常简单，仅用一条45度倾斜的直线即可同时平分阴阳两部分。为了证明这一点，我们只需要计算一下白色的半圆形和45度扇形的面积和即可。二者的面积恰好都等于πR^2/8，其总和为πR^2/4，恰为整个白色区域的一半。由对称性，黑色面积也被平分。除此之外，你还能想到多少种平分方法呢？
1960，Mathematics Magazine杂志编辑C. W. Trigg给出了另外三种解法。一种简单但却很不容易想到的解法是，做一个半径为R/√2的同心圆。这个同心圆的面积恰好是整个圆面积的一半，而由对称性，黑白两部分在小圆内各占一半，在圆环上也各占一半，这说明同心圆确实把两部分面积都平分了。
另一个简单的分法如图4所示，每个小圆都是大圆面积的1/4，因此显然满足要求。图5所示的则是一个很复杂但同时也很具有研究和扩展价值的分法。两个半圆弧的半径分别为R·Φ/2和R·Φ/2 + 1/2，其中Φ为黄金分割(√5-1)/2。可以通过计算验证，这条线确实将黑白二色面积各自平分。注意这种分割法背后的一个重要思想：由于大圆弧的半径始终等于小圆弧半径加上1/2，因此小圆弧半径确定了整个曲线。随着这个半径值的增加，总有一个时候它会恰好平分每一部分的面积。只要这个半径值可以用尺规做出来，我们的问题也就解决了。利用这个思想我们还可以解决一些看似很难办的数学问题，我将在下一篇日志中谈到。
本文来源：http://www.cut-the-knot.org/pythagoras/YinYangBisection.shtml
sofa
别开生面….
沙发没了………………
占不着沙发，坐地板上也不错
喵！
如果是个太极图的话阴阳的分界线应该是个正S嘛:)
matrix67：
你说“1958年，英国数学家Henry Dudeney在他的著作Amusements in Mathematics中曾经提出了这样一个问题……”
我在原文里面并未找到“1958”之处。所以我抱着疑惑查找了一下wikipedia，我猜你说的Henry Dudeney应该是这个人:
亨利·恩斯特·杜德耐（Henry Ernest Dudeney，1857年4月10日~1930年4月24日）
在原文下方reference里面，第一条就是：
1.H. E. Dudeney, AMuzements in Mathematics, Dover, 1970
我猜测那个1970应该是这本书出版的时间。
吹毛求疵了，惭愧惭愧。
这个案例很不错，我准备把它作为明天学校竞赛班培训的第一节的引例。你知道我想了好多素材，都觉得要么太难要么太肤浅，这个真是要好好感谢你！
哦，sorry，我查找了另外的文献发现AMuzements in Mathematics好像最早是1917年出版的，也有说1915年的。呵呵
sofa