（召集）你能想到的最奇妙的算法题是什么？

    昨天和老朋友BY一起吃饭时又一次不可避免地谈到了算法问题。一个有趣的话题是：提起那些最巧妙的、最离奇的牛B算法时，你想到的第一个算法题是什么？

    我第一想到的算法题是那道经典问题：n个数中有且仅有一个数出现了奇数次（其它数都出现了偶数次），如何用线性时间常数空间找出这个数。解法也只有一句话：从头到尾异或一遍，结果就是要求的那个数。该问题的加强版也异常牛B，我曾经在这里介绍过。不过，这个算法我在茶余饭后已经聊过无数次了……

    脑海中出现的另一个牛B算法题则是POJ3318：给你三个n*n的矩阵A、B、C，问你A*B是不是等于C。数据保证O(n^3)铁定超时，因此你需要想一个不用把A和B乘起来就可以验证的算法。一个基于概率的算法是随机生成一个n乘1的矩阵R，然后判断A*B*R是否等于C*R，而前者相当于A*(B*R)，与后者一样都可以在O(n^2)的时间里算出来。如果算出来的结果相等，几乎可以肯定A*B和C也是相等的。


    还想起为高中参加省选的孩子们准备模拟题时挖到的一道可称之为“脑筋急转弯”的算法题：给你一个数列，一次操作是指将某个数移到数列中别的位置上去，然后问最少要几次操作才能让数列变得有序。例如，数列7,1,3,2,6,5就只需要三次移动，把3移到2后面，把5移到6前面，再把7移到最后面即可。当时居然只有一个人想到，这题其实就是一个最长上升子序列问题。因为整个操作过程实质上可以等价地看作是，把要移动的数先全部取出来，再挨个放回适当的位置。这就要求取出要移动的数后，剩下的那些数本身是有序的。若希望要移动的数越少越好，那也就等于说是剩下的不动的数要越多越好。

 
    最近准备一次演讲，翻出了一道旧题，觉得讲起来会相当有意思。当时和BY分享的就是这道题。问题从一个简化版开始：给定一个图，你有一次机会将某条边的权值减半，用O(n^2)的时间求最短路。很多人可能会在第一时间内开始思考，把这次权值减半的机会用到哪里最合适呢？一个明显有欠思考的猜想是，用在边权最小的地方，因为这可以让它更小。事实上，把它用在边权最大的地方显然赚得多，不过问题是，有可能这个边权又太大了，最短路根本就不经过它。一个折衷办法就是，把权值减半的机会用在原图的最短路中的最大边上。这下看上去似乎和谐了，但稍加思索不难发现反例：S到T有两条路径，一条要走99条长为1的边，另一条只需走一条长为100的边。把权值减半的机会用在那条大边上显然更好。
    这题的正确算法呢，其实也不难，预处理S到所有点的最短路，以及T到所有点的最短路，然后枚举每条边，可以直接求出将这条边减半后必须经过该边的最短路（将这条边减半了又不走这条边的人肯定有毛病）。这样，枚举得出的最小值就是我们所求的最短路。
    有趣就有趣在，如果你有k次选一条边令其权值减半的机会，还存在多项式的算法吗？注意，我甚至可以把这k次机会重复用在某些边上，让其权值不断折半。又一个有趣的讨论是，把上面的算法重复套用k次可行吗？换句话说，该题是否具有最优子结构？不见得。下图就是一个反例：k=1时走下面最好，k=2时反而走上面更好。原因就在于，在同一条边上反复减半会越来越亏，还不如把机会分散用在几个权值本来不大的边上。

  

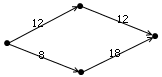
    到底该怎么办呢？其实这题有一个非常巧妙的O(n^2·k^2)的算法，真不知是谁想出来的：把原图分成k+1层，从0到k分别标号。上面的层到下面的层有很多单向边，每条边都和原图上的某条边相对应，跨越了几层权值就打几次对折，表示我“走了一条权值减过的边”。因此，你当前走在第几层，就表示你已经用掉了几次减半机会。在这个有O(nk)个顶点的图上做最短路，其结果就是我们所要求的。

 

    看来，除了几何问题以外，在算法中也有把2D扩展到3D的诡异的思想。图的分层思想很有用，在很多其它问题中也有类似的做法。

 
 
    BY与我分享的则是这样一道题目：在1到n中选取若干个数，要求如果选了x就不能选2x和3x，问共有多少种选择方案。例如，n=3时答案为5，这5种选法分别为{}, {1}, {2}, {3}, {2,3}。我想了很久。BY提示，是动态规划。我又想了很久。BY再提示，是带状态压缩的动态规划。我又想了很久，并且觉得越来越不可思议。后来BY宣布答案，两人立即大笑起来：把数字1放在方阵最左下角，然后不断在一个数的右边填上它的两倍，在其上方填上它的三倍。问题就等价地转化为，在方阵中选取若干个格子使得任意两个不相邻，求有多少种选取方案。这是一个经典的带状态压缩的动态规划问题。另外，遇到尚未出现过的数（即除2和3以外的素数）就再开一张新的表，然后用乘法原理把它们各自对应的方案数乘起来就是了。例如当n=20时，最终答案就等于下面这7张表各自所对应的选取方案数的乘积。

  

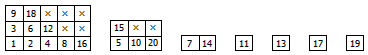
    这题也许还有组合数学方法，但下面这个加强版估计就只能这样做了：如果再给定一些不能选的数，则又有多少种选择方案。

    大家遇到的最神的算法题目又是什么呢？欢迎在下面留意与大家分享！

61 条评论

发表评论




Enter Captcha Here :