趣题：用一副七巧板拼出带有三个洞的图形

    我为最新一期的《博物》杂志写了一篇关于七巧板的文章。文章中我提到了一个有趣的问题：一副七巧板拼出的图形里最多可以有多少个中空的“洞”？Martin Gardner认为，一块副七巧板最多能拼出有三个洞的图形，并且他自己给出了一个非常漂亮的构造。如果你手中有七巧板的话，不妨也来试试看；没有七巧板也不必觉得遗憾，网上遍地都是七巧板Flash游戏。觉得困难的话，不妨先从两个洞开始做起。
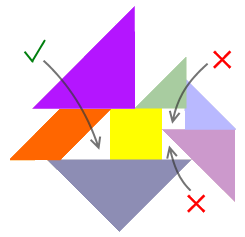
    注意，一个中空的洞必须完全被七巧板的内部空间所包围，仅仅是端点相触由七巧板边界围成的洞是不算的。因此下面的图形中其实只有一个洞，另外两个都不符合规范。

  


 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

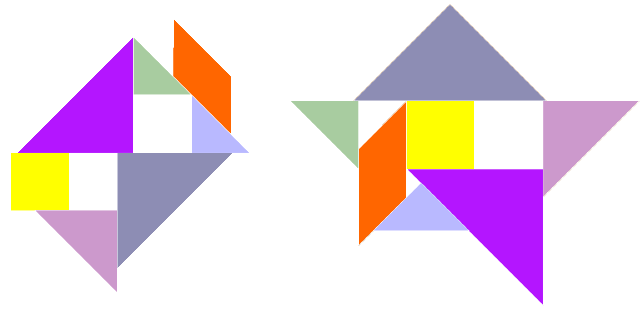
    构造有两个洞的图形相对比较容易（如左图）。构造带有三个洞的图形则相当困难。右图是一个非常精彩的构造，注意顶部大三角形的斜边长为2√2，它所覆盖住的“缺口”长度为2 + 1/√2，前者仅仅比后者多出0.12个单位长度，几乎是刚好把这个缺口封住。

12 条评论

发表评论

  ×  4  =  20