我对各种违背直觉的函数构造特别有兴趣，看看这里你就知道我对这些特殊函数有多痴迷了。因此，当我发现竟然有专门收集各种特殊函数的数学书时，可以想象我的心情有多激动。我试着以“反例”为关键字在图书馆进行检索，借了一大堆实分析数学书。这些书都已经很老了，封皮烂了又烂，已经修修补补重装了两三次封皮。翻翻这些老书，不由得对老一辈的学者和作家表示由衷的崇敬；虽然文字、排版都不出彩，但书的容量极大，内容也很实在。
废话不多说了，让我们来欣赏一下书里的一些精彩篇章吧。
实数域上一个单调递增的有界可微函数f，但lim(x→±∞)f ‘(x)≠0
直觉上，一个单调递增的有界函数走到无穷远的地方一定是“平”的，而事实上却并非如此。我们能构造这样一个函数，它是R上的递增有界函数，但无穷远处的导数并不等于0。
对所有非负整数n，定义f(n)=1 – 1/2^n。接下来，用下面的方式把函数扩张到全体非负实数：对区间(n, n+1)，用一条光滑的、递增的、导数由0变成1再变成0的函数来连接f(n)和f(n+1)（例如正弦函数的一个完整递增区间缩小至原大小的1/2^(n+2)再加上两根分别等于f(n)和f(n+1)的常函数）。
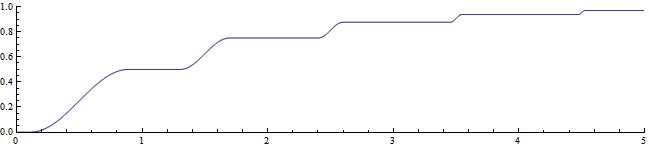
再令f(-x)=-f(x)。则这个函数是R上的一个单调递增的有界函数，但导数的极限显然不为0。事实上，这个函数的导数在无穷远处根本就没有极限，因为不管走到多远导数总能取满从0到1的所有值。
如果把问题的条件改为“严格递增”呢？对于严格递增的有界函数，无穷远处的导数也不见得为0，构造一个反例很简单，只需要在刚才那个函数上面加上一个严格单增的有界函数即可，如令g(x)=f(x)+1-1/2^n。显然，g(x)仍然单调有界，且g'(x)=f'(x) + ln(2)/2^n，其极限仍然不为0。
函数f在x0的任意小的邻域内都无界，但x→x0时f(x)并不趋于无穷大
f(x)=|cos(1/x) / x|满足要求。无论对于多大的正数N，总存在一个充分接近0的点使得f(x)>N。例如，取x=1/(nπ)，则f(x)=|1/x|=nπ，上述结论显然。
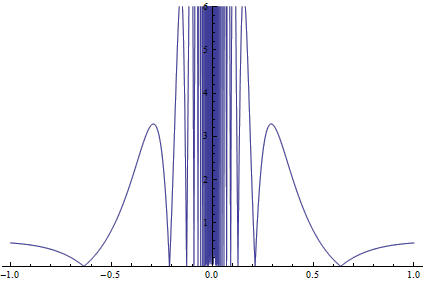
有趣的是，如果取x=1/((n+1/2) π)，则当n→∞时x→0，且f(x)→0。这说明，x趋于0时f(x)并不趋于无穷大。
f(x)→∞，不见得有f ‘(x)→∞
与上例比较类似。考虑(0,1)上的函数f(x)=1/x + cos(1/x)，显然lim(x→0+) f(x)=+∞ 。但f ‘(x)=(sin(1/x)-1)/x^2，若令x=1/(2n+1/2)π，当n→∞时f ‘(x)=0，这说明f ‘(x)→∞是不成立的。
处处有限而又处处局部无界的函数
定义函数f(x)=0 (当x为无理数)， f(x)=n (当x为有理数且可表示为既约分数m/n)。这个函数在每一点上都有意义，每一个f(x)都是有限的；但在任意小的区间内，你能找到分母任意大的既约分数，因此函数在任意小的一个区间上都是无界的。
二元函数f(x,y)在原点处不连续，但在任意一条通过原点的直线上都是连续的
定义函数f(x,y)=x^2/y，当y>0且x^2/y≤1时；f(x,y)=y/x^2，当y>0且x^2/y≥1时；当y=0时f(x,y)=0。再令f(x,-y)=f(x,y)。
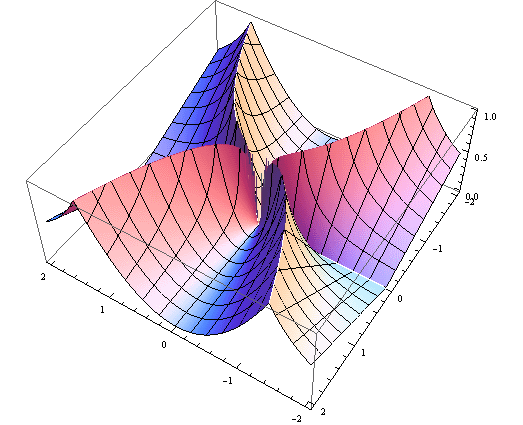
任意接近(0,0)的地方都存在形如(a, a^2)的点，相应的函数值为1，因此函数在原点间断；可是，取任意一条过原点的直线y=mx，当|x|充分小时必有x^2/y≤1，此时|f(x,y)|=|x^2/y|=|x/m|，函数在原点处连续。
T_T m67牛 我能不能和你交个朋友 你太强了
第三条是肯定的吧，不然怎么用罗比达法则呢？
同意LS
推荐本书 拉卡托斯的《证明与反驳》 背景是几何，但是是针对分析的情况写的书。讲这个反例问题和相关的方法论的。
复旦那个版本翻译质量不好，找找那个黑皮的版本，记不清哪的了
事实上，我不觉得这些反例很奇妙～～在数学分析课上见过太多了～～
另外这些反例，诸如f(x)与f'(x)之间的关系，在理论上也没有什么价值
个人认为作为兴趣读物看就可以了
你的中文系课程学得如何？感觉你应该去计算机相关的系
f(x)→∞，不见得有f ‘(x)→∞
这个确实比较扯，随便一个根号x就是了，干嘛搞得那么麻烦
至于最后一个“任意接近(0,0)的地方都存在形如(a, a^2)的点，相应的函数值为1，因此函数在原点间断；”，不明白难道一张曲面上的某点附近有些小孔，这个点就算间断了？
恩，同地幔…
不知道博主有没有系统学习过数学分析（我是说数学专业的那种），如果学过，有些东西是见怪不怪的，我们大学一、二年级就在这里面打滚，现在想想还头皮发麻但是趣味横生。
f(x)→∞，不见得有f ‘(x)→∞
f(x)=x就是反例么
实分析中的反例（上）
（上）？难道还有（下）？
微积分学教程里都有 菲赫金格尔茨
f(x)→∞，不见得有f ‘(x)→∞
也可以用 f(x)=x 、f(x)=x^0.5 和 f(x)=lnx 吧，很直观啊。
“函数f在x0的任意小的邻域内都无界，但x→x0时f(x)并不趋于无穷大”
这时谈不上f(x)趋于什么，这种情况下f（x）无极限定义。
我有一本王昆扬教授新编的《实变函数论》，与周民强先生《实变函数论》不同之处是王老师将普通教材中实变的内容缩减到自编的《数学分析简明教程》中，而他的实变专门讨论实函数的构造性质，如果博主有意，我可以送给你~~
受王老师感染，我从简单的函数开始讨论，比如连续函数的点态性质：
1、存在（0，1）上处处不连续的函数；
2、存在（0，1）上只在一个有限（或可数）点集上连续的函数；
3、不存在（0，1）上只在一个可数稠密集上连续的函数；
4、存在（0，1）上只在一不可数集A上连续的函数，A的补集是不可数集；
5、存在（0，1）上只在一不可数稠密集A上连续的函数，A补集可数稠密；
6、存在（0，1）上在一不可数集A上连续的函数，A补集是不可数集；
7、存在（0，1）上只在一个有限（或可数）点集上不连续的函数；
8、存在（0，1）上连续的函数。
关于这些不知道博主和其他数学同好有没有兴趣一一给出构造或证明~~
建议你用高版本的mathematica把图重新画一下。
楼主辛苦了！！！！
定义函数f(x,y)=x^2/y，当y>0且x^2/y≤1时；f(x,y)=y/x^2，当y>0且x^2/y≥1时；当y=0时f(x,y)=0。再令f(x,-y)=f(x,y)
不要对挫折叹气，姑且把这一切看成是在你成大事之前，必须经受的准备工作。