趣题：扫雷定理 互补棋盘上的数字和相等

    这是一个与扫雷游戏有关的非常好玩的问题。给定一个扫雷布局，定义它的“补集棋盘”为这样一个新布局，原来有雷的地方现在是空地，原来没有雷的地方现在都是雷。在棋盘的每块空地上都标有一个数字，它表示周围的8个方块中有多少颗雷。一个美妙的结论是，两个互补棋盘布局上的数字和是相等的。乍看之下似乎不可思议，但仔细一想便豁然开朗。你能想到这是为什么吗？

  


 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

  

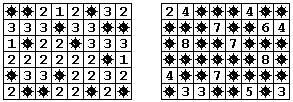
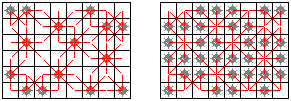
    对于棋盘上的每个空地，在它和它周围的每个雷之间连接一条短线。显然线条的总数目就是棋盘上的数字和。在互补棋盘中，原来的线条现在仍然存在（线条两端原先是一雷一空地，现在仍然是一雷一空地），原来没有线条的地方现在仍然没有（两个邻格或者都有雷或者都是空地，则互补棋盘中依旧如此）。因此，互补棋盘中的线条和原来一模一样，线条总数不变，也即数字和不变。

来源：http://www.cut-the-knot.org/arithmetic/combinatorics/Minesweeper.shtml

20 条评论

发表评论

  +  37  =  43