如果删除字符串A中的若干字母可以得到字符串B，我们就说A包含B（熟悉相关概念的网友可能知道，有一个准确的说法叫做“B是A的子序列”，但为了避免和后面的“序列”混淆，我们不用这种说法）。例如，字符串“matrix”包含了“mix”，也包含“ati”，但不包含“it”。字符串序列aaaaa, ab, bbaa, baaaa, aa, bbacc, cbcacc, bb中的每个字符串都不包含它前面的任何一个字符串，我们称这样的字符串序列为“非生成序列”（我自己取的名字，意思是说任一字符串都不能由前面的项通过添加字母生成出来）。我们可以构造出任意长的非生成序列，例如字符串长度严格递减的序列，或者所有不同的长度为n的字符串。现在的问题是，你能构造出一个无穷长的非生成序列吗？当然，你不能使用无穷多种字母来达到这一点。
你被骗了！事实上，虽然我们能构造出任意长的非生成序列，但我们永远不能构造出无穷长的非生成序列。我们有一个很简单的证明。
假设存在非生成序列，不妨找出所有非生成序列中最“小”的（位于前面的字符串尽可能短的）那一个。换句话说，在所有非生成序列中筛选出第一项最短的，再从中选择出那些第二项最短的，再在剩下的结果中选择序列第三项最短的……由此得到按各项字符串长度来看最靠前的那一个非生成序列。这个序列中有无数多个字符串，但所用到的字母却是有限的；考察所有字符串的首字母，必然有某一个字母出现了无穷多次。不妨设这个字母是“b”，且以b开头的字符串最早出现在第x项。把所有以字母b打头的字符串取出来形成一个临时序列（因此这个临时序列是一个无限长的、每个字符串都以b开头的序列）。删去临时序列中所有字符串的首字母。用这个临时序列替换掉原序列中第x项及其以后的部分。得到的新序列仍是一个无穷多项的非生成序列（倘若新序列中有字符串A可以生成字符串B，则B前面补回一个字母b，或者A和B前面都补上一个“b”，可知原序列中的A也能生成B），但按各项字符串长度来看，它的次序比原来更靠前，矛盾。
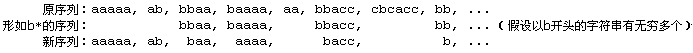
有觉得这个证明有些别扭吗？这是因为，这个证明用到了选择公理。
看了2遍，没看明白。
难怪我想了一个中午，愣是构造不出来，反而能觉得不可能有这种序列。
竟然骗我…
很牛，学习一下。
但是如果字符串长度可以达到无限长，就应该可以吧
来源？
如何构造出任意长的非生成序列？对这个很感兴趣
最后一句话有问题，其实这个证明应该不算用到了选择公理
因为这个问题，显然只能有一个确定的结果，存在或者不存在
但是如果基于选择公理，就应该不确定的结果，直观上无所谓存在不存在
选择公理主要是说，找不到一个直观的选择方法的时候，也肯定有办法从每个集合里选出一个元素，这个是无法证明或者证否的。
但是你这个给出了具体的选择方法，而且是很确定的选择方法，就不会有问题，不用选择公理也可以推出来
“如果删除字符串A中的若干字母可以得到字符串B，我们就说A包含B”
——————————————————
假设把这个“A包含B”的定义改为：
“如果删除字符串A中的开头和/或结尾的若干字母可以得到字符串B，我们就说A包含B”
则“构造无穷长的字符串序列使每一项都不包含它前面的项”是可能的。
地幔说的有理，给出具体的选择方法，就不是在用选择公理了。
地核说的有理，构造方法亦极简单，例如：
11，101，1001，10001，100001，……
证明似乎有点问题，有点类似于下面的证明。
证明，不存在大于0小于1的实数，如果有，那么必然可以找到其中最小的一个，在二进制下记做0.b1b2b3…，由于大于0,所以必然有某个bi=1，则替换成0.b1b2b3…b(i-1)01b(i+2)…可得到更小的实数，矛盾。
最后一句话有问题，其实这个证明应该不算用到了选择公理
因为这个问题，显然只能有一个确定的结果，存在或者不存在
但是如果基于选择公理，就应该不确定的结果，直观上无所谓存在不存在
选择公理主要是说，找不到一个直观的选择方法的时候，也肯定有办法从每个集合里选出一个元素，这个是无法证明或者证否的。
但是你这个给出了具体的选择方法，而且是很确定的选择方法，就不会有问题，不用选择公理也可以推出来
我也很认同这个说法。。
ab,ba,ab,ba,ab…
同意11楼。真的能找出最“小”的无限非生成序列？
11楼有道理。确实错了。