The American Mathematical Monthly新年第一期中有一段精彩的根号2无理性证明。
假设√2等于p/q,那么对于任意自然数n都有:
(√2)n q = 2n/2 q 当n是偶数时
2(n-1)/2 p 当n是奇数时
无论哪种情况,(√2)n q都是一个自然数。由二项式定理,对任意大的n都有:
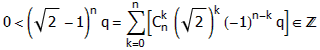
但这显然是不可能的,因为序列(√2 – 1)n q是收敛到0的。
参考资料:http://www.cut-the-knot.org/proofs/sq_root.shtml#proof16
相关文章:五种方法证明根号2是无理数,又一种证明根号2是无理数的方法