下图中的图 (a) 是由三个绳圈组成的。这是一个非常经典的图形,叫做 Borromean rings 。 Borromean rings 有一个非常神奇的特点:它们是套在一起的,没有哪个绳圈能从中取出来;但是,仔细观察你会发现,每两个绳圈之间都并没有直接套在一起!
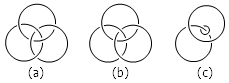
Borromean rings 还有一个听上去更离奇的性质:如图 (b) 所示,如果把其中任意两个绳圈真的套在一起,那么第三个绳圈就会自动脱落掉!为了看出这一点来,我们可以像图 (c) 那样,把其中一个绳圈缩小,让它紧紧地裹在另一个绳圈上,这下就很容易看出,它已经不再对第三个绳圈有任何限制作用了。
为了增强演示时的效果,我们试着把 Borromean rings 中的其中两个绳圈先拉开来,此时第三个绳圈将会变成下图所示的样子。
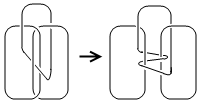
于是,一个小魔术就诞生了。像下图中的左图那样,把一根细线圈缠绕在两个别针上,容易验证这个线圈是取不出来的。现在,把两个别针别在一起,线圈就奇迹般地自己脱落出来了。(你能看出来吗?)
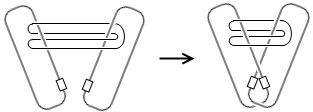
这种违背直觉的东西应该引起大家的警惕。比方说,登山运动员就要小心了:有的时候,把两个绳扣扣在一起,反而会松开套在它们上面的绳子!
参考资料: V. V. Prasolov, Intuitive Topology, Chapter 2
去掉任意一个绳圈,都会解开其他所有的绳圈,满足这种条件的绳圈组叫做 Brunnian link 。 Borromean rings 就是一个最简单的 Brunnian link 。构造更大的 Brunnian link 是一个非常有意思的问题,感兴趣的读者可以看看这里。