偶然瞥见一道很妙的题目:已知三个锐角 α 、 β 、 γ 的和为 90°,求证:sinα + sinβ + sinγ > 1
这个问题的证明方法有很多,不过大家一定会喜欢下面这个证明:
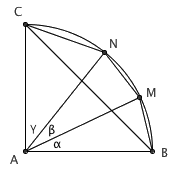
作一个半径为 1 的 90° 扇形,于是图中 α + β + γ = 90° 。注意到 △ABM 的面积可以写成 (1/2) · AB · AM · sinα = sinα / 2,类似地 △AMN 、 △ANC 的面积分别为 sinβ / 2 和 sinγ / 2 ,但他们的面积之和显然大于 △ABC。于是,sinα / 2 + sinβ / 2 + sinγ / 2 > 1/2,即 sinα + sinβ + sinγ > 1 。
这个问题来源于张景中的《数学家的眼光》。