
晚饭之后一起来动动脑吧。纸上有两条夹角很小的直线 a 、 b ,它们在纸外交于一点 O 。在纸上还有一点 P ,大致位置如上图所示。请你利用圆规和(没有刻度的)直尺作出一条同时过 O 、 P 的直线。当然,你不能把图作到纸张外面去。
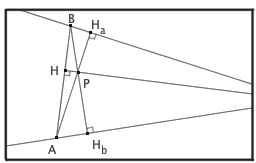
答案:过 P 作直线 a 的垂线,垂足为 Ha ,和 b 交于点 A 。过 P 作直线 b 的垂线,垂足为 Hb ,和 a 交于点 B 。连接 AB 。然后,过 P 作 AB 的垂线 HP ,这条 HP 一定会经过直线 a 、 b 的交点 O 。这是因为, △ABO 的三条高交于一点。
题目来源:CTK Wiki Math
如果你喜欢这个,不妨看几个类似的另类作图趣题:
http://www.matrix67.com/blog/archives/528
http://www.matrix67.com/blog/archives/3513
以及 http://www.matrix67.com/blog/archives/3113 的第 8 题