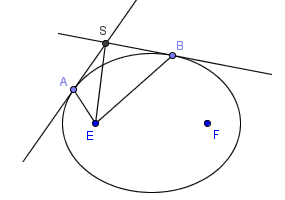
如图,椭圆上A、B两点处的切线相交于S,E是椭圆的一个焦点。求证,线段ES平分∠AEB。
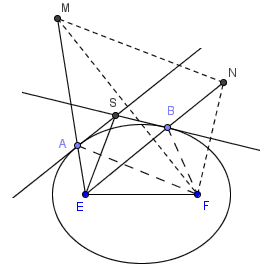
椭圆有一个神奇的性质:从一个焦点射出的光线,经过椭圆曲线的反射后,总会到达另一个焦点。换句话说,两个焦点分别与切点相连,这两条连线与切线夹角相等。再换句话说,将F沿切线AS反射,对称点M恰好落在EA的延长线上;同样地,令N为F关于BS的对称点,则N、B、E三点共线。又由椭圆的定义,EA+FA=EB+FB。于是,我们有:
EM = EA + AM
= EA + FA
= EB + FB
= EB + BN
= EN
这说明△EMN是等腰三角形。为了说明ES为角平分线,只需说明点S也在MN的垂直平分线上即可。这是显然的,因为S是FN和FM的垂直平分线的交点,这立即说明S是△FMN的外心,它当然也应该在MN的垂直平分线上。
几何画板画椭圆及其上的切线很不方便,因此改用GeoGebra了。一个很好的软件,自变/应变元素管理得很好,属性界面用起来非常舒适,命令行操作功能很强大。以后这个Blog讲到几何问题时就靠它来画图了。
题目来源:http://www.cut-the-knot.org/Curriculum/Geometry/AngleBisectorsInEllipse.shtml