房间的正中间悬浮着一个正方形的金属框。五位画家看到这般奇迹后,立即拿出纸和笔,把这个金属框的样子画了下来。但是,由于五位画家观察这个金属框的角度不同,它们画出来的结果也互不相同。请问,这五位画家画出来的结果都是对的吗?换句话说,有没有哪一幅图或者哪几幅图根本不可能是一个正方形的透视图?
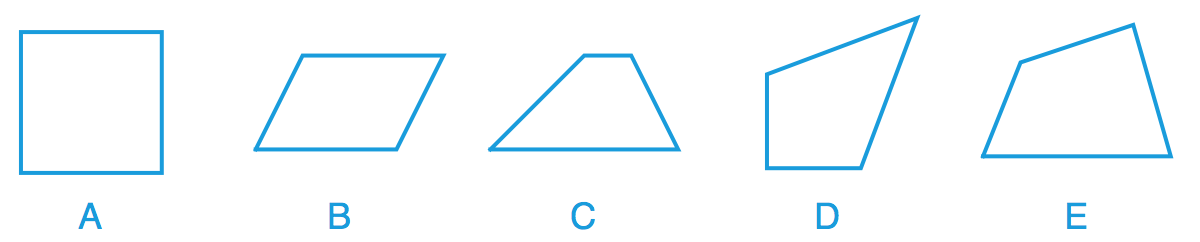
房间的正中间悬浮着一个正方形的金属框。五位画家看到这般奇迹后,立即拿出纸和笔,把这个金属框的样子画了下来。但是,由于五位画家观察这个金属框的角度不同,它们画出来的结果也互不相同。请问,这五位画家画出来的结果都是对的吗?换句话说,有没有哪一幅图或者哪几幅图根本不可能是一个正方形的透视图?

波兰数学家 Wacław Sierpiński 对数论有很多研究。在他一生出版的 50 多本书里, 250 Problems of Elementary Number Theory 一书显得格外有趣。这里面不但有各种出人意料的数学事实,还有很多精妙的证明和大胆的构造,让人大呼过瘾。我从中选择了一些问题,在这里和大家一块儿分享。下面的文字没有完全照搬书中的内容,而是做了大量的改动和扩展;若有出错的地方,还请大家指正。个别题目会涉及一些初等数论中的著名定理,它们都可以在这篇文章里找到。
有时,为了说明某个式子始终成立,我们会为它构造一个情境。例如,为了说明
C(m, 0) · C(w, r) + C(m, 1) · C(w, r – 1) + … + C(m, r) · C(w, 0) = C(m + w, r)
始终成立,只需要注意到,等号的左边和右边计算的都是同一个东西:假如一个班上有 m 个男生 w 个女生,从中选出 r 个人有多少种方案。等号左边的计算方式是,分别计算 0 男 r 女、 1 男 r – 1 女、 2 男 r – 2 女等 r + 1 种情况的方案数,然后把它们加起来。等号右边则是直接算出了从这 m + w 个人中选出 r 个人的方案数。两种算法所得的答案应该是相等的。
现在,请你构造一个情境,来说明不等式
(1 – pm)n + (1 – qn)m ≥ 1
总成立,其中 m 、 n 是任意正整数, p 、 q 是任意正实数,并且满足 p + q ≤ 1 。
大家一定见过很多“我不知道,我也不知道,我还是不知道,我还是不知道,我知道了,我也知道了”的问题。但是,我想大家一定没有见过下面这样的问题。
A 、 B 两人在主持人 C 的带领下玩一个游戏。 C 向两人宣布游戏规则:“一会儿我会随机产生两个不同的形如 n – 1/2k – 1/2k+r 的数,其中 n 、 k 是正整数, r 是非负整数。然后,我会把这两个数分别交给你们。你们每个人都只知道自己手中的数是多少,但不知道对方手中的数是多少。你们需要猜测,谁手中的数更大一些。”这里,我们假设所有人的逻辑推理能力都是无限强的,并且这一点本身也成为了共识。 C 按照规则随机产生了两个数,把它们交给了 A 和 B ,然后问他们是否知道谁手中的数更大。于是有了这样的一段对话。 Read more…
一位画家正在画画。画布上是一望无际的平原,一条笔直的铁路向无限远的地方延伸。画家画了铁路上的两根相邻的枕木,它们在画面上呈两条平行的线段,并且都与地平线平行。这时,画家突然犯难了:根据透视的原理,下一根枕木应该画在哪儿呢?你能帮他确定出下一根枕木的位置吗?

这里,我们假设陆地是一个无限大的平面,并且铁路上的相邻枕木之间的间距相等。