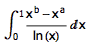某大公司有这么一个规定:只要有一个员工过生日,当天所有员工全部放假一天。但在其余时候,所有员工都没有假期,必须正常上班。这个公司需要雇用多少员工,才能让公司一年内所有员工的总工作时间期望值最大?
假设一年有 365 天,每个员工的生日都概率均等地分布在这 365 天里。
巧解定积分:用定积分来求解定积分
视频:Steiner问题的肥皂膜解法
给定 n 个村庄的位置,要想把他们全部连通,最少需要修建多长的公路?这个问题被称为 Steiner 问题,是由数学家 Jakob Steiner 提出来的。注意,和最小生成树不同的是,公路是可以在中间汇合、分岔的。目前已经知道,Steiner 问题是 NP-hard 的,在规模很大的情况下,不能有效地得出最优解来。
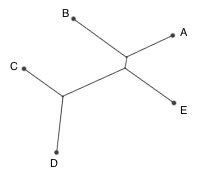
然而,大自然却是无敌的,它可以迅速秒杀这样的难题。由于肥皂膜总会试图让自己的表面积最小,利用肥皂膜实验,我们可以轻易获得 Steiner 问题的解。我在很多书上都看到过肥皂膜实验的方法,不过却从没见过真正的实验视频。今天我终于看到了这样的视频,把它搬进墙来,和大家分享。这个视频也很好地解释了一个普遍存在的误区:说肥皂膜实验一举解决了 NP 问题是不恰当的,因为这个实验只能找到极小值,并不能找到最小值,运气不好的话,实验结果会是失败的。
趣题:和为90度的一组锐角,正弦值之和一定大于1
偶然瞥见一道很妙的题目:已知三个锐角 α 、 β 、 γ 的和为 90°,求证:sinα + sinβ + sinγ > 1
这个问题的证明方法有很多,不过大家一定会喜欢下面这个证明:
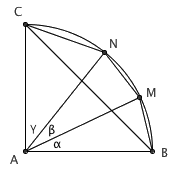
作一个半径为 1 的 90° 扇形,于是图中 α + β + γ = 90° 。注意到 △ABM 的面积可以写成 (1/2) · AB · AM · sinα = sinα / 2,类似地 △AMN 、 △ANC 的面积分别为 sinβ / 2 和 sinγ / 2 ,但他们的面积之和显然大于 △ABC。于是,sinα / 2 + sinβ / 2 + sinγ / 2 > 1/2,即 sinα + sinβ + sinγ > 1 。
这个问题来源于张景中的《数学家的眼光》。
史上最Geek的桌游:ERGO
我先认错,这实在有些标题党了;不过看完游戏规则介绍,我的第一感受确实是这样——这无疑是最适合数学 Geek 的卡牌游戏。在游戏中,玩家们需要轮流出牌,在置牌区中构造出有利于自己的逻辑表达式,证明自己的存在。哈哈,听上去很有意思吧!让我先来详细说说游戏规则。
ERGO 是 2009 年 Catalyst Game Labs 出品的一款桌游。游戏共有 55 张牌,包括:
变量牌 16 张,其中 A 、 B 、 C 、 D 各 4 张
符号牌 20 张,其中 AND 、 OR 、 THEN 各 4 张, NOT 牌 8 张
括号牌 6 张,其中左右括号各 3 张
白板牌 1 张
回转牌 1 张
谬误牌 3 张
辩解牌 3 张
万能牌 2 张,其中变量万能牌和符号万能牌各 1 张
ERGO 牌 3 张