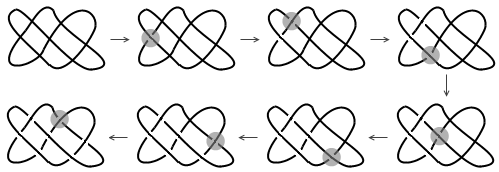
今天听说了 Conway’s Soldiers ，这是 Conway 大牛在 1961 年提出的一个数学谜题（似乎 Conway 的出镜率也太高了），我觉得非常有意思，在这里跟大家介绍一下。内容基本上来自于 Wikipedia 的相关页面。
假设有一个无限大的棋盘。棋盘上可以放置一些象征着士兵的棋子。一个棋子可以跳过并吃掉和它相邻的一枚棋子（就像孔明棋一样）。这是棋子的唯一一种移动方式。现在，在某个位置画一条无限长的水平线，你需要在水平线下面放置足够多的棋子，使得它们前仆后继地往水平线上方跳，最终能够跳到水平线以上 n 个单位的位置。
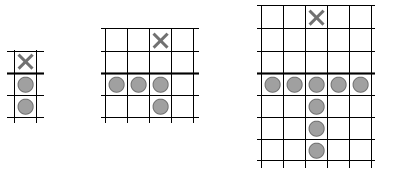
如图所示，当 n = 1 时，两个棋子就够了。当 n = 2 时，我们需要 4 个棋子。当 n = 3 时，最少需要 8 个棋子。
这次的趣题来源于 UyHiP 今年八月份的谜题：概率均等地随机选取一个恰好含有 n 个 0 和 n 个 1 的 2n 位 01 串，这个 01 串平均会有多少个 0 和 1 个数相等的前缀（包括空串和整个串本身）？
为了叙述简便起见，下面我们把所含 0 和 1 个数恰好相等的 01 串叫做平衡的 01 串。例如， 010010110011 就是一个平衡 01 串，它有四个平衡前缀，空串、 01 、01001011 以及整个 01 串本身。我们需要求出的就是，任取一个长为 2n 的平衡 01 串，平衡前缀的个数的期望值是多少。
昨天无聊时用 MPlayer 和 Mathematica 做了一张图。大致过程是，用 MPlayer 从各个电影中提取出间隔大致均等的 600 帧图像，导入到 Mathematica 中，再取各帧图像的颜色平均值，用一根根宽度为 1 像素的竖条来表示。得到的结果就是下面这个样子。你能在看到答案之前先猜出电影名字吗？你能识别出每一段颜色都对应着什么情节吗？
Update: 看了大家的回复，我才悲催地发现，这件事情早有人做过了，而且做得比我更好。大家感兴趣的话可以前往： http://moviebarcode.tumblr.com/
很早以前，我简单介绍过 Julia 集和 Mandelbrot 集，文章在此。这可以说是数学中最神秘、最令人敬畏的研究对象之一。不过，那时我对这个话题了解还不太深。今天见到这个网页，让我对 Julia 集和 Mandelbrot 集有了更深的了解。我查阅了一些其他的资料，然后写下这篇长文，与大家一同分享。继续阅读以前，建议先看看我原来那篇文章（很短），那里面有很多漂亮的 Julia 集和 Mandelbrot 集的图片，这篇文章就不再展示了。
还是让我们先来简单复习一下复数吧。由于承认“负数也能开平方”将会带来很多幽雅和便利的结论，因此我们发明了虚数，用 i 来表示 -1 的平方根（即虚数单位），并把实数扩展为复数（即一切形如 a + b i 的数）。正如实数可以用数轴上的点来表示一样，复数可以用平面直角坐标系上的点来表示。令 x 轴表示复数的实数部分，令 y 轴表示复数的虚数部分，则 a + b i 就对应了平面上的点 (a, b) 。我们把这个平面直角坐标系叫做“复平面”。
A Midsummer Knot’s Dream 简直可以说是去年学术界的一篇奇文，大家点进去看看就知道了。论文里讲了一个基于纽结理论的双人对弈游戏，名字也非常有艺术感： To Knot or Not to Knot 。这个游戏可能是最难的组合游戏了，它的数学性极强，思考难度非常大，甚至比 ERGO 更不容易上手。一场游戏下来，究竟谁赢谁输可能都不好判断。
To Knot or Not to Knot 的游戏规则非常简单。用铅笔在纸上画一个封闭的、可以自相交的回路，然后 A 、 B 两人轮流在图形中选取一个尚未被处理过的交叉点，并用橡皮擦对图形进行“细化”，明确两根线条的位置关系（可以抛掷硬币决定谁先行动）。A 的目的是要让最终的图形变成一个结，而 B 的目的则是避免图形打结。下面是其中一种可能的游戏过程，双方约定 B 先走。两人轮流对交叉点进行细化，七步之后，整个图形并未打结（你能看出来吗）， B 获得胜利。
注意，这是一个决策透明、信息公开的游戏，并且游戏不可能有平局产生。因此，即使双方都使出最佳策略，也必然有一个人会赢有一个人会输。也就是说，任意给定一个初始状态，总有一方有必胜的策略。不过，难就难在，究竟谁有必胜策略，必胜策略是什么，这并不容易判断。让我们来做一个练习题吧：下面的图形中，如果 A 先走，B 后走，谁有必胜策略？如果 B 先走，A 后走呢？记住，A 的任务是要让最终的图形打成结，而 B 的任务则是避免图形打结。
