环面多面体,即亏格为 1 的多面体,直观地说就是有 1 个洞的多面体。下图中三个多面体里分别有 0 个洞、1 个洞和 2 个洞。第二个多面体就是环面多面体。最近,我在研究一些和环面多面体相关的话题,在这里和大家分享一些我的发现。
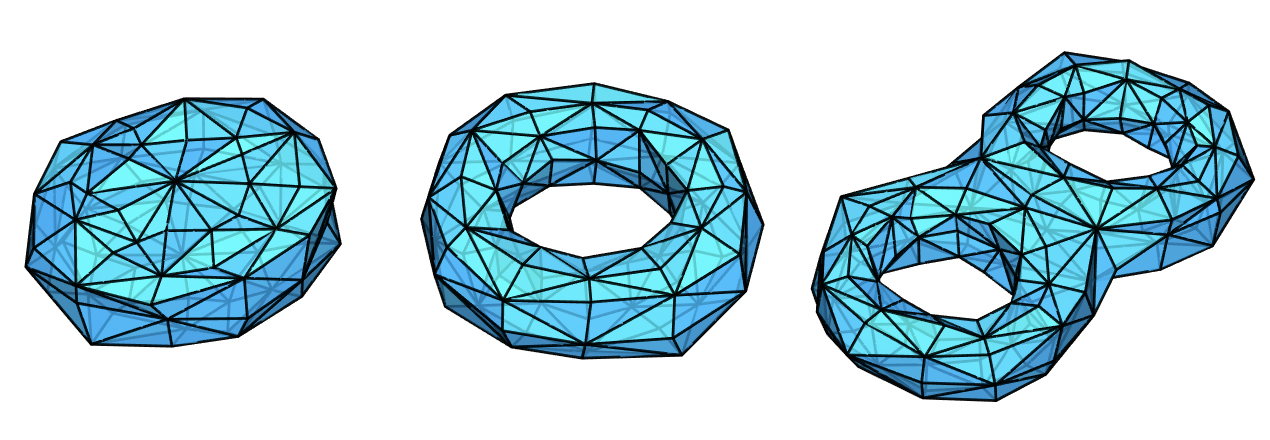
环面多面体,即亏格为 1 的多面体,直观地说就是有 1 个洞的多面体。下图中三个多面体里分别有 0 个洞、1 个洞和 2 个洞。第二个多面体就是环面多面体。最近,我在研究一些和环面多面体相关的话题,在这里和大家分享一些我的发现。

我正在餐桌前吃早餐。餐桌上有一张圆形的大饼,有一个方形的蛋糕,还有一个甜甜圈。我依次思考了下面三个问题。你能帮我想出它们的答案吗?
提示:上一个问题的答案总会为下一个问题提供线索。
大家应该听说过 9 枚硬币的问题吧。9 枚硬币当中有 8 枚是真币,有 1 枚是假币。所有的真币重量都相同,假币的重量则稍重一些。怎样利用一架天平两次就找出哪一枚硬币是假币?方法是,先把 9 枚硬币分成三组,每组各 3 枚硬币。然后,把第一组放在天平左边,把第二组放在天平右边。如果天平向左倾斜,说明假币在第一组里;如果天平向右倾斜,说明假币在第二组里;如果天平平衡,说明假币在剩下的第三组里。现在,假币的嫌疑范围就被缩小到 3 枚硬币之中了。选择其中 2 枚硬币分放在天平左右两侧。类似地,如果天平左倾,就说明左边那枚硬币是假的;如果天平右倾,就说明右边那枚硬币是假的;如果天平平衡,就说明没放上去的那枚硬币是假的。
9 硬币问题实在是太经典了,你甚至能在人教版小学五年级下册的课本里看到它。9 硬币问题还衍生出了很多变形,其中最著名的当属 12 硬币问题了:有 12 枚硬币,其中一枚是假币,但我们不知道假币是更重一些还是更轻一些;请利用一架天平三次找出哪一枚硬币是假币,并判断出它比真币更重还是更轻。12 硬币问题的经典程度恐怕不亚于 9 硬币问题。早在 20 世纪 40 年代,12 硬币问题就已经吸引了一大批数学家和数学爱好者,甚至有人建议把这个问题扔到德国去,以削弱德国人在二战中的战斗力。如果你想知道答案,可以在网上找找,应该很容易找到。我们今天就不讨论了。
今天,我们真正想聊的其实是这个问题的另外一种比较少见的变形:仍然是要在 9 枚硬币当中寻找 1 枚假币,仍然假设假币的重量要稍重一些,仍然只能使用天平两次;但是这一次,你所使用的是一种“天平机”,它不会立即告诉你现在是哪边重哪边轻,而是在你两次称完后把这两次的结果一并打印给你。这下,你就没法根据天平的反馈结果随机应变了,必须事先把每次怎么放硬币全规划好。那么,你该怎么办?在本文后面的内容中,均已知假币比真币更重,直至另有说明。
下面这个趣题出自 Using your Head is Permitted 谜题站 2016 年 10 月的题目:能否把一个凸四边形分成若干个凹四边形?
随着常数 m 和 n 的变化,参数方程 x = sin(m · t), y = sin(n · t) 将会画出一系列漂亮的曲线。法国物理学家 Jules Antoine Lissajous 曾在 1857 年研究过这类曲线,因此人们把它叫做 Lissajous 曲线。我在 reddit 上看到了一个 Lissajous 曲线的动画演示,觉得看起来确实非常爽;但那个动画里没有解释曲线的生成方法,很多细节也有让人不太满意的地方,于是决定自己制作一个。这个动画展示的是 m = 13, n = 18 时的 Lissajous 曲线。