在下面的问题中，你不能使用圆规，只能使用直尺作图。不过，你的直尺拥有两条平行边，你可以在作图时同时使用它们。你需要充分利用直尺的这个特点，完成下面几个作图任务。
1. 作出已知角的角平分线；
2. 作出已知线段的中点；
3. 作出已知圆的圆心；
4. 过已知点作已知直线的平行线。
假设你的直尺是无限长的。直尺的宽度是固定不变的。直尺不能用来度量长度。
用抛物线筛选质数
今天见到一种看上去很帅的质数筛选法。在平面直角坐标系上画出抛物线 y = x2 的图像，然后标出抛物线上的所有格点（两坐标均为整数的点）。其中，只有点 (0, 0) 正好在 y 轴上，其余的点要么在 y 轴左侧，要么在 y 轴右侧。把 y 轴左侧除了 (-1, 1) 以外的所有格点与 y 轴右侧除了 (1, 1) 以外的所有格点相连，这些连线将自动避开 y 轴上纵坐标为质数的点。连接足够多的线条之后，质数就逐渐露了出来。
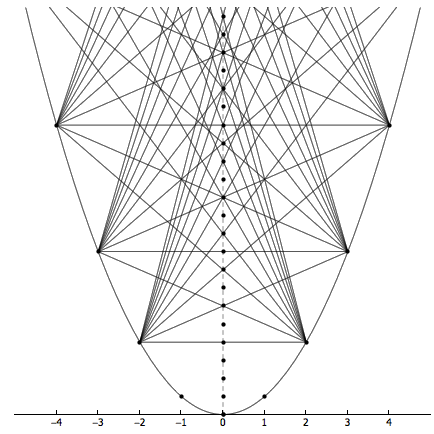
这是因为， (-a, a2) 和 (b, b2) 的连线将经过 (0, a · b) ，这可以通过计算斜率的方法得到验证。这个颇具创意的质数筛选法叫做 visual sieve ，它是由 Yuri Matiyasevich 和 Boris Stechkin 提出的。
查看更多：
http://plus.maths.org/content/catching-primes
http://www.mathteacherctk.com/blog/2011/10/the-parabolic-sieve-of-prime-numbers/
UyHiP趣题：按照盒子的三边长之和来计费有没有漏洞？
今天的趣题来自 UyHiP 今年十月的趣题。
许多快递公司都依据物件的长、宽、高三边之和来收费，一些航空公司也要求托运行李的三边长相加不能超过某个限制。那么是否有人想过，有没有可能把一个三边之和较大的盒子装进一个三边之和较小的盒子里，从而骗取更低的费用呢？有人会说，恐怕不行吧，长宽高之和更大的盒子体积不也应该更大一些吗？不见得。比方说，盒子 A 的长宽高分别是 10 、 10 、 10 ，盒子 B 的长宽高分别是 9 、 9 、 12.1 。盒子 B 的三边长之和显然比盒子 A 要大，但体积只有 980.1 ，比前者要小近 20 个单位。那么，为什么就不能把盒子 B 沿斜线方向塞进盒子 A 呢？有人会敏锐地发现，在上面的例子中，盒子 A 的体对角线长为 17.3205 ，但盒子B的对角线长度达到 17.5616 ，显然无法完全放进盒子 A 里。不过且慢，我也能举出这样的例子，三边和更大的盒子其体积和对角线都比小的盒子的要小。盒子 A 的长宽高分别为 10 、 10 、 20 ，盒子 B 的长宽高分别为 7.1 、 16.5 、 16.5 。盒子 B 的长宽高之和比盒子 A 大，体积为 1932.98 ，对角线长度比前者小大约 0.1 。看来，为了解决这个问题，我们还需要从一些更巧妙的方面入手。
趣题：只允许加倍操作的水桶倒水问题
今天的题目来自这里。有三个水桶，它们里面分别装了 a 升的水、 b 升的水和 c 升的水（其中 a 、 b 、 c 都是正整数，桶本身没有容量限制）。你可以把水从一个桶倒进另一个桶，但必须保证让后者的水量刚好变成原来的两倍。证明，不管 a 、 b 、 c 是多少，你总能让其中某一个水桶变空。
例如，假设初始时 (a, b, c) = (3, 2, 1) ，那么你可以先把 (3, 2, 1) 变成 (1, 4, 1) ，再把它变成 (2, 4, 0) ，从而把第三个水桶变空。
无聊小制作：“数词+非数词+数词+非数词”的出现频数
昨天和同事聊到，汉语还真是奇怪，有“四分五裂”，有“五颜六色”，也有“七上八下”，但好像从没听说过六什么七什么的。于是想到，在汉语中，“数词 + 非数词 + 数词 + 非数词”的短语是怎样分布的呢？回到家后立即用 Mathematica 做了一个柱状图，绘出了九九八十一种数词短语模式在大规模真实语料中的出现频数。注意，这里统计的是总的出现频数，重复出现也会计算在内。另外，这是一个简单而机械的统计过程，因而 “三人一组”、“七天七夜”之类的非成语也被算了进来。
嗯，对，没有任何意义，纯属无聊之作。