考虑这么一个 14 位数 02565413989732 ，如图所示，它的数字先逐渐变大，然后开始变小，再变大，再变小，再变大，再变小。我们就说，它一共包含了 6 个单调区间。我们的问题就是：一个 n 位数平均有多少个单调区间？为了避免歧义，我们假设任意两位相邻的数字都不相同，因而像 77765589911 这样的数我们就不考虑了。另外，大家可能已经注意到了，我们允许这个 n 位数以数字 0 开头。因而，更精确地说，我们的问题是：相邻数字都不相同的、允许以 0 开头的所有 n 位数当中，平均有多少个单调区间？
这个题目来自 1987 年 IMO 候选题。
下图中的图 (a) 是由三个绳圈组成的。这是一个非常经典的图形，叫做 Borromean rings 。 Borromean rings 有一个非常神奇的特点：它们是套在一起的，没有哪个绳圈能从中取出来；但是，仔细观察你会发现，每两个绳圈之间都并没有直接套在一起！
Borromean rings 还有一个听上去更离奇的性质：如图 (b) 所示，如果把其中任意两个绳圈真的套在一起，那么第三个绳圈就会自动脱落掉！为了看出这一点来，我们可以像图 (c) 那样，把其中一个绳圈缩小，让它紧紧地裹在另一个绳圈上，这下就很容易看出，它已经不再对第三个绳圈有任何限制作用了。
证明：对于任意一个三角形和任意一个大于等于 4 的正整数 n ，都存在一种把这个三角形分割成 n 个等腰三角形的方案。这个问题曾经出现在 1976 年的 Crux Mathematicorum 上。 1977 年， Gali Salvatore 给出了一个非常漂亮的解答。
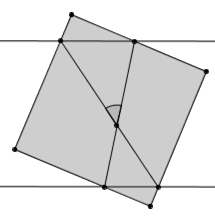
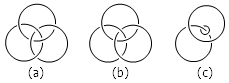
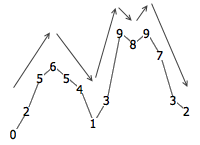你或许熟知一个非常经典的结论： Fibonacci 数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … （头两项都是 1 ，此后每一项都是前两项之和）的相邻两项之比将会越来越接近黄金比例 0.618 ，不信请看：
1 / 1 = 1.0000000…
1 / 2 = 0.50000000…
2 / 3 = 0.66666667…
3 / 5 = 0.60000000…
5 / 8 = 0.62500000…
8 / 13 = 0.61538462…
13 / 21 = 0.61904762…
21 / 34 = 0.61764706…
34 / 55 = 0.61818182…
55 / 89 = 0.61797753…
89 / 144 = 0.61805556…
144 / 233 = 0.61802575…
… …
Fibonacci 数列究竟是怎么和黄金比例扯上关系的？一个简单的解释就是，假设相邻两项之比存在一个极限，那么到了无穷远的时候，连续的三个数 a, b, a + b 将会满足 a / b = b / (a + b) ，这正好就是黄金比例的定义。我最近用 Mathematica 做了一组动画，尝试着用图形化的方法更直观地展示 Fibonacci 数列和黄金比例之间的联系。
