如果叫我说出一个我最喜欢的数学定理，之前我可能会说 Monge 定理；不过现在，我可能会说 Marden 定理了：
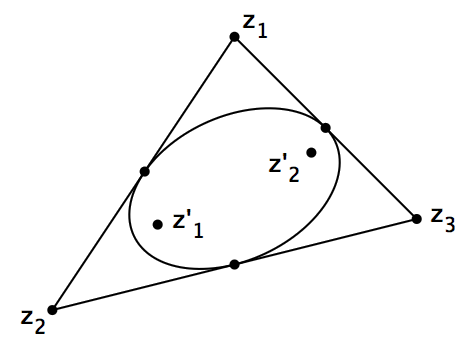
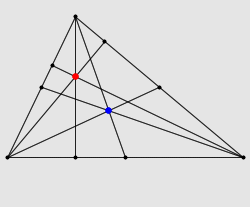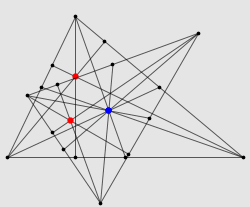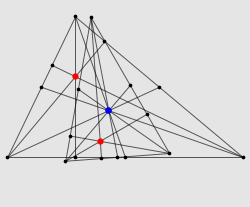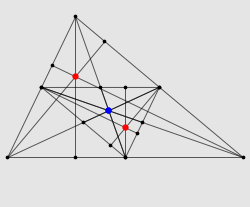
设 p(z) 是一个复数域上的三次多项式， z1 、 z2 、 z3 是 p(z) 的三个根，它们在复平面上不共线。那么，在这个复平面上存在唯一的椭圆，使得它与三角形 z1z2z3 的各边都相切，并且都切于各边的中点处。并且，这个椭圆的两个焦点是 p'(z) 的两根。
读完这个结论以后，你一定会被数学之美深深地打动。这个结论出现在了 Morris Marden 于 1945 年发表的一篇论文里，因而被 Dan Kalman 称为 Marden 定理。 Marden 本人则认为，这个结论最早是由 Jörg Siebeck 在 1864 年发现并证明的。下面我们简单地来证明一下这个结论，证明过程出自 Dan Kalman 在 2008 年发表的获奖论文 An Elementary Proof of Marden’s Theorem 。
在早期的小型图像编辑软件中，考虑到时间空间的限制，再加上算法本身的难度，很多看似非常简单的功能都无法实现。比如说，很多图像编辑软件只允许用户把所选的内容旋转 90 度、 180 度或者 270 度，不支持任意度数的旋转。毕竟，如果我们只是旋转 90 度的整数倍，那么所有像素仅仅是在做某些有规律的轮换，这甚至不需要额外的内存空间就能完成。但是，如果旋转别的度数，那么在采样和反锯齿等方面都将会有不小的挑战。
不过， Windows 自带的画图软件聪明地用 skew 功能（中文版翻译成“扭曲”）部分地填补了无法自由变形的缺陷。随便选中图中的一块区域，再在菜单栏上选择“图像”→“拉伸/扭曲”，然后在“水平扭曲”那儿填写一个 -89 到 89 之间的整数（表示一个角度值），再按一下确定，于是整个图形就会像下图所示的那样被拉斜，其中 θ 就是你刚才填的度数。如果你填入的 θ 是负数值，则倾斜的方向会与下图方向相反。类似地，“垂直扭曲”功能会在竖直方向上对图形进行拉扯，如果角度值为正数，则整个图形会变得左低右高，如果角度值为负数，则整个图形会变得左高右低。
不过，这玩意儿对于我们来说似乎完全没用。估计 99% 的人在使用画图软件的时候就从来没用过这个功能吧。如果真是这样，那么今天的问题恐怕将会是大家最近一段时间见过的最有趣的问题了：想办法利用 Windows 画图中的扭曲功能（近似地）实现 28 度旋转。
任意一个三角形的三条中线都会交于一点，这个点就叫做三角形的“重心”。任意一个三角形的三条高都会交于一点，这个点就叫做三角形的“垂心”。任意一个三角形三边的垂直平分线都会交于一点，这个点就叫做三角形的“外心”。 1765 年，大数学家 Euler 指出：任意一个三角形的重心、垂心和外心都在一条直线上，并且重心会把垂心和外心的连线分成 2 : 1 两段。这个结论虽然有很多很漂亮的证明，但作为一个非常基本的结论，它还有一种非常直观的解释方法。最近在做一个课件的时候，需要用到这种直观理解的动画演示，结果在网上找了半天也没找到，最终决定自己做了一个。
上图中，红色的点是三角形三条高的交点，也就是垂心；蓝色的点是三角形三条中线的交点，也就是重心。现在，把整个三角形绕着重心旋转 180 度，同时以重心为中心把图形缩小到原来的一半。于是，每个点都会跑到重心的正对面去，同时到重心的距离也会缩短到原来的一半。你会发现，由此得到的小三角形，三个顶点都在大三角形各边的中点处（因为它们是大三角形的顶点转过来得到的，而重心在各中线的 2 : 1 处）；同时，小三角形的三条高分别与大三角形的各边垂直（因为它们是大三角形的高转了 180 度得到的）。你会发现，小三角形的垂心正好就是大三角形的外心！而小三角形的垂心就是由大三角形的垂心转过来得到的，这两个点与重心应该在一条线上，并且到重心的距离有 1 : 2 的关系。这样一来，我们就相当于证明了 Euler 线定理。
还记得小时候有一道经典奥数题，大概是让你把两个数字 1 、两个数字 2 、两个数字 3 和两个数字 4 排成一个 8 位数，使得其中两个数字 1 之间正好夹着 1 个数字，两个数字 2 之间正好夹着 2 个数字，两个数字 3 之间正好夹着 3 个数字，两个数字 4 之间正好夹着 4 个数字。稍作尝试便可得出正确答案： 4, 1, 3, 1, 2, 4, 3, 2 。如果把逆序后的数列视作本质相同的数列，那么上面这个答案是唯一的。这个问题是由 C. Dudley Langford 在 1958 年提出的，因此我们把它叫做 Langford 数列。
当 n = 3 时， Langford 数列也是唯一的： 2, 3, 1, 2, 1, 3 。我小时候曾经没日没夜地试图寻找 n = 5 时的 Langford 数列，结果却怎么也找不到。后来才知道， n = 5 时的 Langford 数列根本就不存在。这是为什么？你能证明这一点吗？
在一棵树中，任意两个顶点之间的路径都是唯一的。如果一棵树有 n 个顶点，那么这棵树总共会有 n(n-1)/2 条路径（每两个顶点都会确定出一条路径来）。 1975 年， John Leech 提出了这么一个问题：有多少顶点数为 n 且边上带权的树，使得图中所有 n(n-1)/2 条路径的权值之和正好是 1, 2, …, n(n-1)/2 ？Leech 本人给出了五个这样的例子，其中四个如下图所示，顶点数 n 分别为 2 、 3 、 4 、 4 。第五棵满足要求的树拥有 6 个顶点，把它找出来将会是一个不小的挑战，感兴趣的读者不妨尝试一下，本文最后会公布答案。 Leech 注意到了 n = 5 时是无解的，但却并没有给出一个解释。
1977 年， Herbert Taylor 给出了一个非常漂亮的解释：如果一棵树满足上述要求，那么顶点数 n 一定是形如 m2 或者 m2 + 2 的数。让我们来看一看这个精妙的证明。
