用 k × 1 的小矩形覆盖一个 n × n 的正方形棋盘,往往不能实现完全覆盖(比如,有时候 n × n 甚至根本就不是 k 的整倍数)。不过,在众多覆盖方案中,总有一种覆盖方案会让没有覆盖到的方格个数达到最少,我们就用 m(n, k) 来表示这个数目。求证:不管 n 和 k 是多少, m(n, k) 一定是一个完全平方数。
趣题:圆中的两个相切的半圆
下面这个结论是 Andrew Jobbings 在 2011 年指出的:
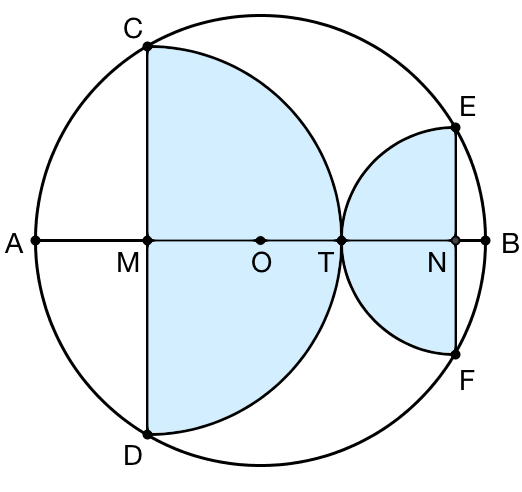
AB 是圆 O 的一条直径, CD 、 EF 是两条垂直于 AB 的弦,并且以 CD 为直径的半圆和以 EF 为直径的半圆正好切于点 T 。那么,两个半圆的面积之和一定等于圆 O 的面积的一半。
你能证明这个结论吗?
杨辉三角中的自然底数 e
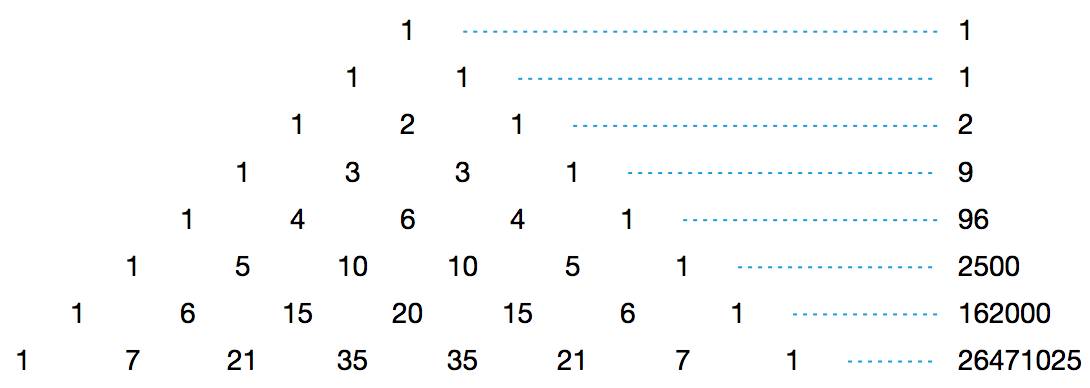
你相信吗,杨辉三角里竟然也有自然底数 e 的身影。 2012 年, Harlan Brothers 发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第 n 行的所有数之积记作 sn ,那么随着 n 的增加, sn · sn+2 / sn+12 会越来越接近 e ≈ 2.718 。事实上,我们有:
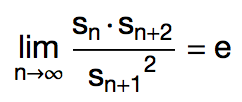
这是为什么呢? John Baez 在这个网页上给出了一个漂亮的解释。
保加利亚单人纸牌游戏
保加利亚单人纸牌游戏(Bulgarian solitaire)的玩法如下:
取出 45 张牌,然后把它们随意分成若干堆。接下来,从每一堆里各取一张牌,叠在一起形成一堆新的牌。不断这样做下去,如果某个时候桌面上正好有 9 堆牌,并且各堆牌数分别为 1, 2, 3, 4, …, 9 ,你就获胜了。
乍看上去,如果初始局面设定不佳,游戏很可能会陷入某个循环,从而永远无法获胜。然而, 1981 年,丹麦数学家 Jørgen Brandt 证明了,对于任意一个初始局面(包括把所有牌摆成 1 堆,以及把所有牌分成 45 堆这样的极端局面),游戏都能在有限步之内获胜。事实上,如果把 45 换成任意一个三角形数 n = 1 + 2 + … + k ,结论仍然成立。
通信复杂度问题:利用特殊机器判断公共元素的存在性
某个导师要和 A 、 B 两名学生玩一个游戏。导师会把 A 、 B 两名学生分别放进两间小黑屋里,每间屋子里都有一台电脑,这两台电脑之间只有一条通信线路。然后,导师会想一个正整数 n (可能会非常非常大),把它的值告诉这两名学生;再构造出集合 {1, 2, …, n} 的两个子集,分别交给这两名学生。于是,每个人都知道了 n 的值和 {1, 2, …, n} 的一个子集。两人需要合作确定出,他们手中的集合是否包含公共的元素。他们之间交流信息的唯一途径就是那条通信线路,但他们能够使用的流量是有限的。具体能够使用多少 bit 的流量,这可以由他们自己决定,但必须在游戏开始之前(也就是 n 的值确定之前)就定好并告诉导师。
和其他类似的问题一样,在游戏开始之前,两人可以商量一个对策。不过,这一回,两人商量了很久,始终无法找到一个必胜的对策。就在两人快放弃的时候,他们突然发现,两人的通信线路上存在一个“漏洞”:两人都可以不计流量地访问一台特殊的第三方机器,我们不妨把它叫做机器 O 。不过,机器 O 只能做一件事情:从 A 那儿读取一个 1 到 n 的排列,从 B 那儿读取一个 1 到 n 的排列,然后计算出这两个排列复合之后是否恰好含有一个循环,并将计算结果分别告知 A 和 B 。然后,机器 O 就会自动关机,再也不能访问了。也就是说,A 和 B 只能使用机器 O 一次。注意, A 、 B 两人是无法看到对方传给机器 O 的数据的,另外机器 O 只能用于处理 1 到 n 之间的排列,不能处理其他大小的排列。