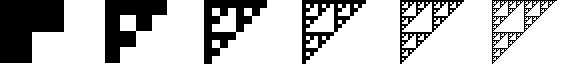在所有的分形图形中，Sierpinski三角形可能是大家最熟悉的了，因为它在OI题目中经常出现，OJ上的题目和省选题目中都有它的身影。这篇文章将简单介绍Sierpinski三角形的几个惊人性质。如果你以前就对Sierpinski三角形有一些了解，这篇文章带给你的震撼将更大，因为你会发现Sierpinski三角形竟然还有这些用途。

Sierpinski三角形的构造
      
    和之前介绍的两种图形一样，Sierpinski三角形也是一种分形图形，它是递归地构造的。最常见的构造方法如上图所示：把一个三角形分成四等份，挖掉中间那一份，然后继续对另外三个三角形进行这样的操作，并且无限地递归下去。每一次迭代后整个图形的面积都会减小到原来的3/4，因此最终得到的图形面积显然为0。这也就是说，Sierpinski三角形其实是一条曲线，它的Hausdorff维度介于1和2之间。

    Sierpinski三角形的另一种构造方法如下图所示。把正方形分成四等份，去掉右下角的那一份，并且对另外三个正方形递归地操作下去。挖个几次后把脑袋一歪，你就可以看到一个等腰直角的Sierpinski三角形。

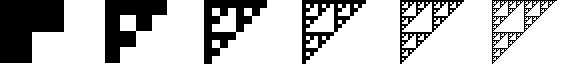
    Sierpinski三角形有一个神奇的性质：如果某一个位置上有点（没被挖去），那么它与原三角形顶点的连线上的中点处也有点。这给出另一个诡异的Sierpinski三角形构造方法：给出三角形的三个顶点，然后从其中一个顶点出发，每次随机向任意一个顶点移动1/2的距离（走到与那个顶点的连线的中点上），并在该位置作一个标记；无限次操作后所有的标记就组成了Sierpinski三角形。下面的程序演示了这一过程，程序在fpc 2.0下通过编译。对不起用C语言的兄弟了，我不会C语言的图形操作。
{$ASSERTIONS+}

   x:=x1;
   y:=y1;
   for i:=1 to density do
   begin
      r:=random(3);
      if r=0 then
      begin
         x:=(x+x1)/2;
         y:=(y+y1)/2;
      end
      else if r=1 then
      begin
         x:=(x+x2)/2;
         y:=(y+y2)/2;
      end
      else begin
         x:=(x+x3)/2;
         y:=(y+y3)/2;
      end;
      PutPixel(round(x),round(y),white);
      Delay(timestep);
   end;
   CloseGraph;
end.

Sierpinski三角形与杨辉三角
    第一次发现Sierpinski三角形与杨辉三角的关系时，你会发现这玩意儿不是一般的牛。写出8行或者16行的杨辉三角，然后把杨辉三角中的奇数和偶数用不同的颜色区别开来，你会发现杨辉三角模2与Sierpinski三角形是等价的。也就是说，二项式系数（组合数）的奇偶性竟然可以表现为一个分形图形！在感到诧异的同时，冷静下来仔细想想，你会发现这并不难理解。
      
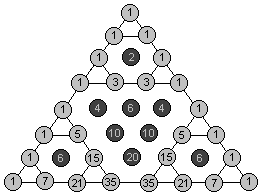
    我们下面说明，如何通过杨辉三角奇偶表的前四行推出后四行来。可以看到杨辉三角的前四行是一个二阶的Sierpinski三角形，它的第四行全是奇数。由于奇数加奇数等于偶数，那么第五行中除了首尾两项为1外其余项都是偶数。而偶数加偶数还是偶数，因此中间那一排连续的偶数不断地两两相加必然得到一个全是偶数项的“倒三角”。同时，第五行首尾的两个1将分别产生两个和杨辉三角前四行一样的二阶Sierpinski三角形。这正好组成了一个三阶的Sierpinski三角形。显然它的最末行仍然均为奇数，那么对于更大规模的杨辉三角，结论将继续成立。

Sierpinski三角形与Hanoi塔
    有没有想过，把Hanoi塔的所有状态画出来，可以转移的状态间连一条线，最后得到的是一个什么样的图形？二阶Hanoi塔反正也只有9个节点，你可以自己试着画一下。不断调整节点的位置后，得到的图形大概就像这个样子：
      
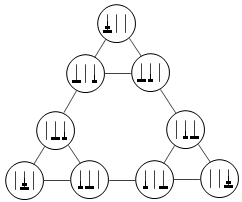
    如果把三阶的Hanoi塔表示成无向图的话，得到的结果就是三阶的Sierpinski三角形。下面的这张图说明了这一点。把二阶Hanoi塔对应的无向图复制两份放在下面，然后在不同的柱子上为每个子图的每个状态添加一个更大的盘子。新的图中原来可以互相转移的状态现在仍然可以转移，同时还出现了三个新的转移关系将三个子图连接在了一起。重新调整一下各个节点的位置，我们可以得到一个三阶的Sierpinski三角形。
  
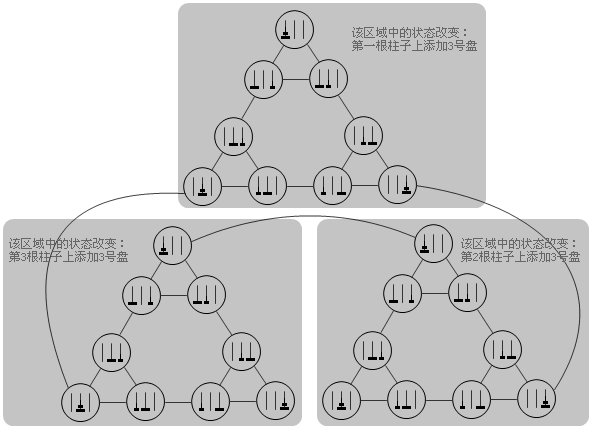
    显然，对于更大规模的Hanoi塔问题，结论仍然成立。

Sierpinski三角形与位运算
    编程画出Sierpinski三角形比想象中的更简单。下面的两个代码（实质相同，仅语言不同）可以打印出一个Sierpinski三角形来。
const
   n=1 shl 5-1;
var
   i,j:integer;
begin
   for i:=0 to n do
   begin
      for j:=0 to n do
         if i and j = j then write('#')
         else write(' ');
      writeln;
   end;
   readln;
end.
#include <stdio.h>
int main()
{
    const int n=(1<<5)-1;
    int i,j;
    for (i=0; i<=n; i++)
    {
        for (j=0; j<=n; j++)
           printf( (i&j)==j ? "#" : " ");
        printf("n");
    }    
    getchar();
 &n
bsp;  return 0;
}
    上面两个程序是一样的。程序将输出：
#                              
##                              
# #                            
####                            
#   #                          
##  ##                          
# # # #                        
########                        
#       #                      
##      ##                      
# #     # #                    
####    ####                    
#   #   #   #                  
##  ##  ##  ##                  
# # # # # # # #                
################                
#               #              
##              ##              
# #             # #            
####            ####            
#   #           #   #          
##  ##          ##  ##          
# # # #         # # # #        
########        ########        
#       #       #       #      
##      ##      ##      ##      
# #     # #     # #     # #    
####    ####    ####    ####    
#   #   #   #   #   #   #   #  
##  ##  ##  ##  ##  ##  ##  ##  
# # # # # # # # # # # # # # # #
################################

    这个程序告诉我们：在第i行第j列上打一个点当且仅当i and j=j，这样最后得到的图形就是一个Sierpinski三角形。这是为什么呢？其实原因很简单。把i和j写成二进制（添加前导0使它们位数相同），由于j不能大于i，因此只有下面三种情况：
    情况一：
    i = 1?????
    j = 1?????
    问号部分i大于等于j
    i的问号部分记作i'，j的问号部分记作j'。此时i and j=j当且仅当i' and j'=j'

    情况二：
    i = 1?????
    j = 0?????
    问号部分i大于等于j
    i的问号部分记作i'，j的问号部分记作j'。此时i and j=j当且仅当i' and j'=j'

    情况三：
    i = 1?????
    j = 0?????
    问号部分i小于j
    此时i and j永远不可能等于j。i' < j'意味着i'和j'中首次出现数字不同的那一位上前者为0，后者为1，那么i和j做and运算时这一位的结果是0，与j不等。

    注意到，去掉一个二进制数最高位上的“1”，相当于从这个数中减去不超过它的最大的2的幂。观察每一种情况中i,j和i',j'的实际位置，不难发现这三种情况递归地定义出了整个Sierpinski三角形。
    嘿！发现没有，我通过Sierpinski三角形证明了这个结论：组合数C(N,K)为奇数当且仅当N and K=K。这篇文章很早之前就计划在写了，前几天有人问到这个东西，今天顺便也写进来。
    另外，把i and j=j 换成i or j=n也可以打印出Sierpinski三角形来。i and j=j表示j的二进制中有1的位置上i也有个1，那么此时i or (not j)结果一定全为1（相当于程序中的常量n），因此打印出来的结果与原来的输出正好左右镜像。

Matrix67原创
转贴请注明出处

网友Voldemort在12楼和13楼很辛苦地帖了一个杨辉三角模2问题的扩展，大家可以看看