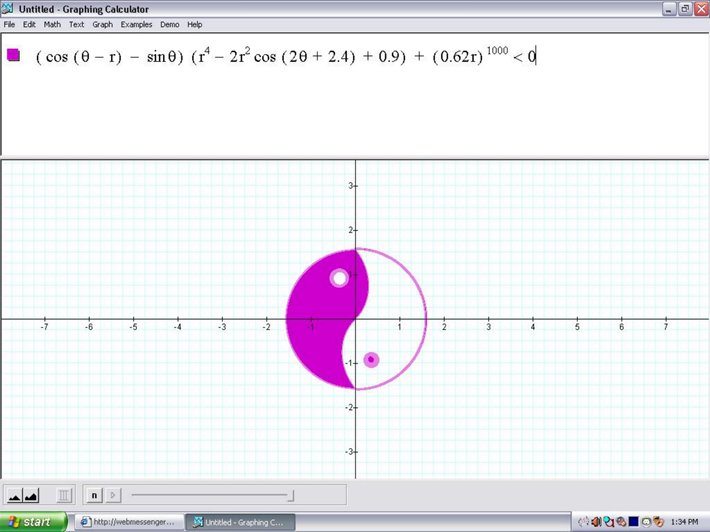
刚才在网上发现了上面这张猛图。急着想验证一下,但不知道Mathematica如何画极坐标的隐函数,于是写了一个Free Pascal的小程序。大家也可以试着把这个小程序粘贴到Free Pascal里运行一下看看。
Read more…

刚才在网上发现了上面这张猛图。急着想验证一下,但不知道Mathematica如何画极坐标的隐函数,于是写了一个Free Pascal的小程序。大家也可以试着把这个小程序粘贴到Free Pascal里运行一下看看。
Read more…
一个正整数n的阶乘就是前n个正整数的乘积,我们通常需要n-1次乘法操作来算出精确的值。不像等差数列求和、a的n次幂之类的东西,目前求阶乘还没有什么巨牛无比的高效算法,我们所能做的仅仅是做一些小的优化。
更少的乘法运算次数?
在高精度运算中,乘法计算的速度远远慢于加减法,因此我们有必要减少乘法运算的次数。下面我将做一个非常简单的变换,使得计算阶乘只需要n/2次乘法。继续看下去之前,你能自己想到这个算法来吗?
我们可以把一个数的阶乘转换为若干个平方差的积。例如,假如我想求9!,我可以把前9个正整数的乘积写成这个样子:
1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9
= (5-4) * (5-3) * (5-2) * (5-1) * 5 * (5+1) * (5+2) * (5+3) * (5+4)
= (5-1) * (5+1) * (5-2) * (5+2) * (5-3) * (5+3) * (5-4) * (5+4) * 5
= (5^2 – 1^2) * (5^2 – 2^2) * (5^2 – 3^2) * (5^2 – 4^2) * 5
注意到一个有趣的事实:上面的四个平方差算出来分别是24, 21, 16, 9,它们之间的差正好是连续的奇数(因为n^2等于前n个正奇数的和)。因此,我们可以用初始数(n/2)^2不断减去一个个的正奇数,求出所有n/2个平方差,再用n/2次乘法把它们乘起来。这种算法实现起来非常简单,并且(当n不大时)同样只需要单精度乘高精度,但需要的乘法次数大大减少了。假设我们已经有了一个高精度类,求n!只需要下面几句话:long h=n/2, q=h*h;
long r = (n&1)==1 ? 2*q*n : 2*q;
f = LargeInteger.create(r);
for(int d=1; d<n-2; d+=2)
f = f.multiply(q-=d);
更少的总运算次数?
尽量提取阶乘中的因子2,我们可以得到另一种阶乘运算的优化方法。这很可能是不需要分解质因数的阶乘算法中最快的一种。
假如我们需要计算20!,我们可以把20拆成若干组正奇数的乘积:
1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 11 * 12 * 13 * 14 * 15 * 16 * 17 * 18 * 19 * 20
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 2 * 4 * 6 * 8 * 10 * 12 * 14 * 16 * 18 * 20
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 2^10
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 2 * 4 * 6 * 8 * 10 * 2^10
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 2 * 3 * 4 * 5 * 2^15
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 2 * 4 * 2^15
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 1 * 2 * 2^17
= 1 * 3 * 5 * 7 * 9 * 11 * 13 * 15 * 17 * 19 * 1 * 3 * 5 * 7 * 9 * 1 * 3 * 5 * 1 * 2^18
只需要一次累乘就可以求到每一组奇数的乘积,最后再花费log(n)次乘法把它们全部乘起来。最后的那个2^18也可以二分计算出来。真正的代码还有很多细节上的优化,另外还借用了递归使得操作变得更加简便。你可以在本文最后附的那个链接里去找Split-Recursive算法。
还能再快一点么?
继续扩展上面的算法,我们可以想到,如果把每个数的质因数都分解出来,并且统计每种质因子有多少个,我们就可以多次使用二分求幂,再把它们的结果乘起来。注意这里并不是真的要老老实实地去分解每个数的质因子。对于每个质数x,我们可以很快算出前n个正整数一共包含有多少个质因子x(记得如何求n!末尾有多少个0么)。这种算法的效率相当高,已经能够满足大多数人的需要了。
另一种诡异的阶乘算法:
这个算法可能是所有有名字的阶乘算法中最慢的一个了(Additive Moessner算法),它对一个数列进行重复的累加操作,一次次地计算前缀和,总共将花费O(n^3)次加法操作。但是,令人费解的是,这个简单的程序为什么可以输出前n个正整数的阶乘呢?a[0]:=1;
for i:=1 to n do
begin
a[i]:=0;
for j:=n downto 1 do
begin
for k:=1 to j do
a[k]:=a[k]+a[k-1]
write(a[i],' ');
end;
end;
我在网上搜索相关的东西时找到了另一个有趣的东西。对一个初始时全为1的数列反复进行这两个操作:累加求前缀和,然后以1,2,3,…的间隔划掉其中一部分数(即划去所有位置编号为三角形数的数)形成新的序列。类似的数列操作方法最先由Alfred Moessner提出的,我们这里不妨把它叫做Moessner数列。你会发现,第n轮操作开始前,数列的第一个数恰好是n! 。看看下面的例子吧:
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 …
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 …
x 2 x 4 5 x 7 8 9 x 11 12 13 14 x …
2 4 5 7 8 9 11 12 13 14 …
2 6 11 18 26 35 46 58 71 85 …
x 6 x 18 26 x 46 58 71 x …
6 18 26 46 58 71 …
6 24 50 96 154 225 …
x 24 x 96 154 x …
24 96 154 …
24 120 274 …
x 120 x …
120 …
…..
当然,发现前面O(n^3)的程序和这个Moessner数列的关联时我很是吃了一惊:在前面的程序里,如果你输出每一次i循环末所得到的数列,你会发现输出的这些数正好就是后面这个问题里被我们划掉的数,而它们其实就是第一类Stirling数!
这到底是为什么呢?是什么东西把阶乘、第一类Stirling数、Moessner数列和那个O(n^3)的程序联系在一起的呢?昨天,我想这个问题想了一天,最后终于想通了。如果把Moessner数列排列成这个样子,一切就恍然大悟了:
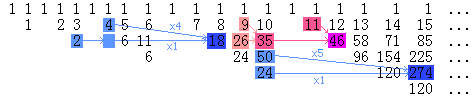
仔细观察上图,我们会发现:
1. 按照Moessner数列的定义,每个数都应该等于它左边的数和左上角的数的和(这个“左边”可以跳过若干空格)。例如,35 = 9 + 26,46 = 11 + 35。排成一系列三角形后,每个三角形最右边一列的数就是被划去的数,它永远不能参与它下面的那些行的运算。
2. 设a[n,i,j]表示左起第n个三角形阵列中的第i行右起第j列上的数,则a[n,i,j]=a[n-1,i-1,j]*n + a[n-1,i,j],例如274=50*5+24。如果递推时遇到空白位置而它左边隔若干空格的地方还有数的话,则需要用左边的数来补,例如18=4*4+2。对于每个三角形的最后一列来说,这个性质实际上就是第一类Stirling数的递推关系,因此Moessner数列中才会出现第一类Stirling数。
3. 在第一类Stirling数中,s(n,1)=n! ,也即左起第n个三角形最底端的那个数等于n!。从上面的第二个性质来看,这也是显然的。
4. O(n^3)的算法实际上就是在绘制上面这个图。每一次j循环末,我们得到
的序列是第i个三角形中每一行左起第j个数组成的序列。例如,计算第5个三角形内的数时,程序首先累加出1, 11, 46, 96, 120, 120,这样便算出了a[5]=120,数列的前5个数再次累加即得到1, 12, 58, 154, 274,由此算出a[4]=274。
第二个性质可以利用第一个性质进行数学归纳法证明,证明很简单,我就不多说了。现在我尽可能少写一些繁琐的细节,节约一些时间用来复习古代汉语。
做人要厚道,
转贴请注明出处。
查看更多:
http://www.luschny.de/math/factorial/FastFactorialFunctions.htm
http://www.luschny.de/math/factorial/index.html <—- 巨牛,20多种阶乘算法的代码!
考虑函数f(z)=z^2-0.75。固定z0的值后,我们可以通过不断地迭代算出一系列的z值:z1=f(z0), z2=f(z1), z3=f(z2), …。比如,当z0 = 1时,我们可以依次迭代出:
z1 = f(1.0) = 1.0^2 – 0.75 = 0.25
z2 = f(0.25) = 0.25^2 – 0.75 = -0.6875
z3 = f(-0.6875) = (-0.6875)^2 – 0.75 = -0.2773
z4 = f(-0.2773) = (-0.2773)^2 – 0.75 = -0.6731
z5 = f(-0.6731) = (-0.6731)^2 – 0.75 = -0.2970
…
可以看出,z值始终在某一范围内,并将最终收敛到某一个值上。
但当z0=2时,情况就不一样了。几次迭代后我们将立即发现z值最终会趋于无穷大:
z1 = f(2.0) = (2.0)^2 – 0.75 = 3.25
z2 = f(3.25) = (3.25)^2 – 0.75 = 9.8125
z3 = f(9.8125) = (9.8125)^2 – 0.75 = 95.535
z4 = f(95.535) = (95.535)^2 – 0.75 = 9126.2
z5 = f(9126.2) = (9126.2)^2 – 0.75 = 83287819.2
…
经过计算,我们可以得到如下结论:当z0属于[-1.5, 1.5]时,z值始终不会超出某个范围;而当z0小于-1.5或大于1.5后,z值最终将趋于无穷。
现在,我们把这个函数扩展到整个复数范围。对于复数z0=x+iy,取不同的x值和y值,函数迭代的结果不一样:对于有些z0,函数值约束在某一范围内;而对于另一些z0,函数值则发散到无穷。由于复数对应平面上的点,因此我们可以用一个平面图形来表示,对于哪些z0函数值最终趋于无穷,对于哪些z0函数值最终不会趋于无穷。我们用深灰色表示不会使函数值趋于无穷的z0;对于其它的z0,我们用不同的颜色来区别不同的发散速度。由于当某个时候|z|>2时,函数值一定发散,因此这里定义发散速度为:使|z|大于2的迭代次数越少,则发散速度越快。这个图形可以编程画出。和上次一样,我用Pascal语言,因为我不会C的图形操作。某个MM要过生日了,我把这个自己编程画的图片送给她^_^
{$ASSERTIONS+}
uses graph;
type
complex=record
re:real;
im:real;
end;
operator * (a:complex; b:complex) c:complex;
begin
c.re := a.re*b.re - a.im*b.im;
c.im := a.im*b.re + a.re*b.im;
end;
operator + (a:complex; b:complex) c:complex;
begin
c.re := a.re + b.re;
c.im := a.im + b.im;
end;
var
z,c:complex;
gd,gm,i,j,k:integer;
begin
gd:=D8bit;
gm:=m640x480;
InitGraph(gd,gm,'');
Assert(graphResult=grOk);
c.re:=-0.75;
c.im:=0;
for i:=-300 to 300 do
for j:=-200 to 200 do
begin
z.re:=i/200;
z.im:=j/200;
for k:=0 to 200 do
begin
if sqrt(z.re*z.re + z.im*z.im) >2 then break
else z:=(z*z)+c;
end;
PutPixel(i+300,j+200,k)
end;
readln;
CloseGraph;
end.
代码在Windows XP SP2,FPC 2.0下通过编译,麻烦大家帮忙报告一下程序运行是否正常(上次有人告诉我说我写的绘图程序不能编译)。在我这里,程序运行的结果如下:
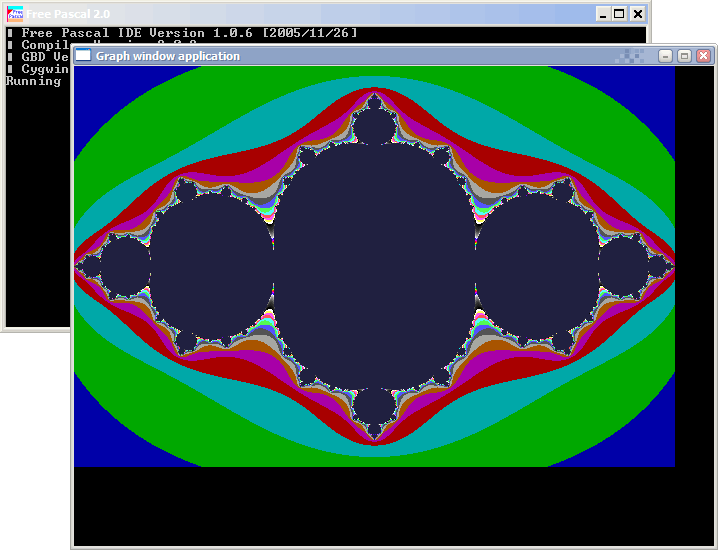
这个美丽的分形图形表现的就是f(z)=z^2-0.75时的Julia集。考虑复数函数f(z)=z^2+c,不同的复数c对应着不同的Julia集。也就是说,每取一个不同的c你都能得到一个不同的Julia集分形图形,并且令人吃惊的是每一个分形图形都是那么美丽。下面的六幅图片是取不同的c值得到的分形图形。你可能不相信这样一个简单的构造法则可以生成这么美丽的图形,这没什么,你可以改变上面程序代码中c变量的值来亲自验证。
c = 0.45, -0.1428

c = 0.285, 0.01
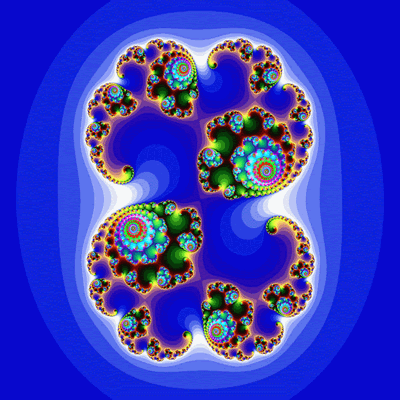
c = 0.285, 0

c = -0.8, 0.156

c = -0.835, -0.2321

c = -0.70176, -0.3842
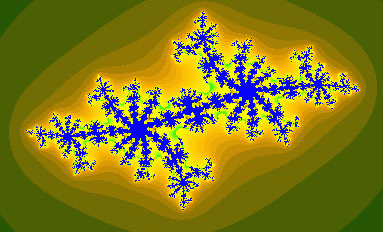
类似地,我们固定z0=0,那么对于不同的复数c,函数的迭代结果也不同。由于复数c对应平面上的点,因此我们可以用一个平面图形来表示,对于某个复数c,函数f(z)=z^2+c从z0=0开始迭代是否会发散到无穷。我们同样用不同颜色来表示不同的发散速度,最后得出的就是Mandelbrot集分形图形:

前面说过,分形图形是可以无限递归下去的,它的复杂度不随尺度减小而消失。Mandelbrot集的神奇之处就在于,你可以对这个分形图形不断放大,不同的尺度下你所看到的景象可能完全不同。放大到一定时候,你可以看到更小规模的Mandelbrot集,这证明Mandelbrot集是自相似的。下面的15幅图演示了Mandelbrot集的一个放大过程,你可以在这个过程中看到不同样式的分形图形。



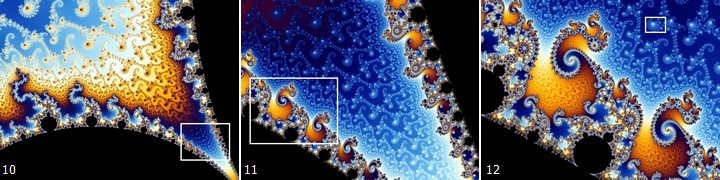

网上可以找到很多小程序实现Mandelbrot集的放大过程。把上面给出的代码改一改,你也可以写出一个这样的程序来。
Update:2011 年 8 月 31 日,我对这个话题做了更进一步的讨论 http://www.matrix67.com/blog/archives/4570
在所有的分形图形中,Sierpinski三角形可能是大家最熟悉的了,因为它在OI题目中经常出现,OJ上的题目和省选题目中都有它的身影。这篇文章将简单介绍Sierpinski三角形的几个惊人性质。如果你以前就对Sierpinski三角形有一些了解,这篇文章带给你的震撼将更大,因为你会发现Sierpinski三角形竟然还有这些用途。
Sierpinski三角形的构造

和之前介绍的两种图形一样,Sierpinski三角形也是一种分形图形,它是递归地构造的。最常见的构造方法如上图所示:把一个三角形分成四等份,挖掉中间那一份,然后继续对另外三个三角形进行这样的操作,并且无限地递归下去。每一次迭代后整个图形的面积都会减小到原来的3/4,因此最终得到的图形面积显然为0。这也就是说,Sierpinski三角形其实是一条曲线,它的Hausdorff维度介于1和2之间。
Sierpinski三角形的另一种构造方法如下图所示。把正方形分成四等份,去掉右下角的那一份,并且对另外三个正方形递归地操作下去。挖个几次后把脑袋一歪,你就可以看到一个等腰直角的Sierpinski三角形。
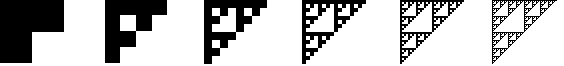
Sierpinski三角形有一个神奇的性质:如果某一个位置上有点(没被挖去),那么它与原三角形顶点的连线上的中点处也有点。这给出另一个诡异的Sierpinski三角形构造方法:给出三角形的三个顶点,然后从其中一个顶点出发,每次随机向任意一个顶点移动1/2的距离(走到与那个顶点的连线的中点上),并在该位置作一个标记;无限次操作后所有的标记就组成了Sierpinski三角形。下面的程序演示了这一过程,程序在fpc 2.0下通过编译。对不起用C语言的兄弟了,我不会C语言的图形操作。{$ASSERTIONS+}
uses graph,crt;
const
x1=320; y1=20;
x2=90; y2=420;
x3=550; y3=420;
density=2500;
timestep=10;
var
gd,gm,i,r:integer;
x,y:real;
begin
gd:=D8bit;
gm:=m640x480;
InitGraph(gd,gm,'');
Assert(graphResult=grOk);
x:=x1;
y:=y1;
for i:=1 to density do
begin
r:=random(3);
if r=0 then
begin
x:=(x+x1)/2;
y:=(y+y1)/2;
end
else if r=1 then
begin
x:=(x+x2)/2;
y:=(y+y2)/2;
end
else begin
x:=(x+x3)/2;
y:=(y+y3)/2;
end;
PutPixel(round(x),round(y),white);
Delay(timestep);
end;
CloseGraph;
end.
Sierpinski三角形与杨辉三角
第一次发现Sierpinski三角形与杨辉三角的关系时,你会发现这玩意儿不是一般的牛。写出8行或者16行的杨辉三角,然后把杨辉三角中的奇数和偶数用不同的颜色区别开来,你会发现杨辉三角模2与Sierpinski三角形是等价的。也就是说,二项式系数(组合数)的奇偶性竟然可以表现为一个分形图形!在感到诧异的同时,冷静下来仔细想想,你会发现这并不难理解。
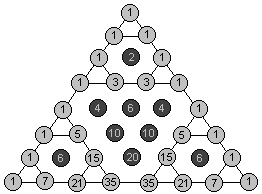
我们下面说明,如何通过杨辉三角奇偶表的前四行推出后四行来。可以看到杨辉三角的前四行是一个二阶的Sierpinski三角形,它的第四行全是奇数。由于奇数加奇数等于偶数,那么第五行中除了首尾两项为1外其余项都是偶数。而偶数加偶数还是偶数,因此中间那一排连续的偶数不断地两两相加必然得到一个全是偶数项的“倒三角”。同时,第五行首尾的两个1将分别产生两个和杨辉三角前四行一样的二阶Sierpinski三角形。这正好组成了一个三阶的Sierpinski三角形。显然它的最末行仍然均为奇数,那么对于更大规模的杨辉三角,结论将继续成立。
Sierpinski三角形与Hanoi塔
有没有想过,把Hanoi塔的所有状态画出来,可以转移的状态间连一条线,最后得到的是一个什么样的图形?二阶Hanoi塔反正也只有9个节点,你可以自己试着画一下。不断调整节点的位置后,得到的图形大概就像这个样子:
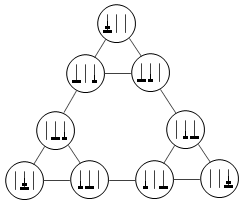
如果把三阶的Hanoi塔表示成无向图的话,得到的结果就是三阶的Sierpinski三角形。下面的这张图说明了这一点。把二阶Hanoi塔对应的无向图复制两份放在下面,然后在不同的柱子上为每个子图的每个状态添加一个更大的盘子。新的图中原来可以互相转移的状态现在仍然可以转移,同时还出现了三个新的转移关系将三个子图连接在了一起。重新调整一下各个节点的位置,我们可以得到一个三阶的Sierpinski三角形。
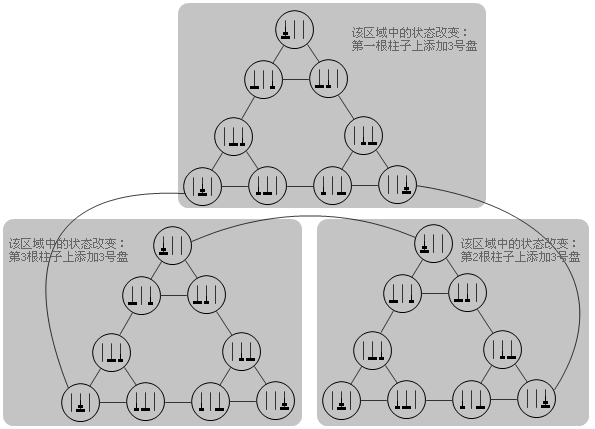
显然,对于更大规模的Hanoi塔问题,结论仍然成立。
Sierpinski三角形与位运算
编程画出Sierpinski三角形比想象中的更简单。下面的两个代码(实质相同,仅语言不同)可以打印出一个Sierpinski三角形来。const
n=1 shl 5-1;
var
i,j:integer;
begin
for i:=0 to n do
begin
for j:=0 to n do
if i and j = j then write('#')
else write(' ');
writeln;
end;
readln;
end.#include <stdio.h>
int main()
{
const int n=(1<<5)-1;
int i,j;
for (i=0; i<=n; i++)
{
for (j=0; j<=n; j++)
printf( (i&j)==j ? "#" : " ");
printf("n");
}
getchar();
&n
bsp; return 0;
}
上面两个程序是一样的。程序将输出:#
##
# #
####
# #
## ##
# # # #
########
# #
## ##
# # # #
#### ####
# # # #
## ## ## ##
# # # # # # # #
################
# #
## ##
# # # #
#### ####
# # # #
## ## ## ##
# # # # # # # #
######## ########
# # # #
## ## ## ##
# # # # # # # #
#### #### #### ####
# # # # # # # #
## ## ## ## ## ## ## ##
# # # # # # # # # # # # # # # #
################################
这个程序告诉我们:在第i行第j列上打一个点当且仅当i and j=j,这样最后得到的图形就是一个Sierpinski三角形。这是为什么呢?其实原因很简单。把i和j写成二进制(添加前导0使它们位数相同),由于j不能大于i,因此只有下面三种情况:
情况一:
i = 1?????
j = 1?????
问号部分i大于等于j
i的问号部分记作i',j的问号部分记作j'。此时i and j=j当且仅当i' and j'=j'
情况二:
i = 1?????
j = 0?????
问号部分i大于等于j
i的问号部分记作i',j的问号部分记作j'。此时i and j=j当且仅当i' and j'=j'
情况三:
i = 1?????
j = 0?????
问号部分i小于j
此时i and j永远不可能等于j。i' < j'意味着i'和j'中首次出现数字不同的那一位上前者为0,后者为1,那么i和j做and运算时这一位的结果是0,与j不等。
注意到,去掉一个二进制数最高位上的“1”,相当于从这个数中减去不超过它的最大的2的幂。观察每一种情况中i,j和i',j'的实际位置,不难发现这三种情况递归地定义出了整个Sierpinski三角形。
嘿!发现没有,我通过Sierpinski三角形证明了这个结论:组合数C(N,K)为奇数当且仅当N and K=K。这篇文章很早之前就计划在写了,前几天有人问到这个东西,今天顺便也写进来。
另外,把i and j=j 换成i or j=n也可以打印出Sierpinski三角形来。i and j=j表示j的二进制中有1的位置上i也有个1,那么此时i or (not j)结果一定全为1(相当于程序中的常量n),因此打印出来的结果与原来的输出正好左右镜像。
Matrix67原创
转贴请注明出处
网友Voldemort在12楼和13楼很辛苦地帖了一个杨辉三角模2问题的扩展,大家可以看看
下面分享的是我自己写的三个代码,里面有些题目也是我自己出的。这些代码都是在我的Pascal时代写的,恕不提供C语言了。代码写得并不好,我只是想告诉大家位运算在实战中的应用,包括了搜索和状态压缩DP方面的题目。其实大家可以在网上找到更多用位运算优化的题目,这里整理出一些自己写的代码,只是为了原创系列文章的完整性。这一系列文章到这里就结束了,希望大家能有所收获。
Matrix67原创,转贴请注明出处。
Problem : 费解的开关
题目来源
06年NOIp模拟赛(一) by Matrix67 第四题问题描述
你玩过“拉灯”游戏吗?25盏灯排成一个5×5的方形。每一个灯都有一个开关,游戏者可以改变它的状态。每一步,游戏者可以改变某一个灯的状态。游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字“1”表示一盏开着的灯,用数字“0”表示关着的灯。下面这种状态10111
01101
10111
10000
11011在改变了最左上角的灯的状态后将变成:
01111
11101
10111
10000
11011再改变它正中间的灯后状态将变成:
01111
11001
11001
10100
11011给定一些游戏的初始状态,编写程序判断游戏者是否可能在6步以内使所有的灯都变亮。
输入格式
第一行有一个正整数n,代表数据中共有n个待解决的游戏初始状态。
以下若干行数据分为n组,每组数据有5行,每行5个字符。每组数据描述了一个游戏的初始状态。各组数据间用一个空行分隔。
对于30%的数据,n<=5;
对于100%的数据,n<=500。输出格式
输出数据一共有n行,每行有一个小于等于6的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态,若6步以内无法使所有灯变亮,请输出“-1”。样例输入
3
00111
01011
10001
11010
1110011101
11101
11110
11111
1111101111
11111
11111
11111
11111样例输出
3
2
-1
程序代码const
BigPrime=3214567;
MaxStep=6;
type
pointer=^rec;
rec=record
v:longint;
step:integer;
next:pointer;
end;
var
total:longint;
hash:array[0..BigPrime-1]of pointer;
q:array[1..400000]of rec;
function update(a:longint;p:integer):longint;
begin
a:=a xor (1 shl p);
if p mod 5<>0 then a:=a xor (1 shl (p-1));
if (p+1) mod 5<>0 then a:=a xor (1 shl (p+1));
if p<20 then a:=a xor (1 shl (p+5));
if p>4 then a:=a xor (1 shl (p-5));
exit(a);
end;
function find(a:longint;step:integer):boolean;
var
now:pointer;
begin
now:=hash[a mod BigPrime];
while now<>nil do
begin
if now^.v=a then exit(true);
now:=now^.next;
end;
new(now);
now^.v:=a;
now^.step:=step;
now^.next:=hash[a mod BigPrime];
hash[a mod BigPrime]:=now;
total:=total+1;
exit(false);
end;
procedure solve;
var
p:integer;
close:longint=0;
open:longint=1;
begin
find(1 shl 25-1,0);
q[1].v:=1 shl 25-1;
q[1].step:=0;
repeat
inc(close);
for p:=0 to 24 do
if not find(update(q[close].v,p),q[close].step+1) and (q[close].step+1<MaxStep) then
begin
open:=open+1;
q[open].v:=update(q[close].v,p);
q[open].step:=q[close].step+1;
end;
until close>=open;
end;
procedure print(a:longint);
var
now:pointer;
begin
now:=hash[a mod BigPrime];
while now<>nil do
begin
if now^.v=a then
begin
writeln(now^.step);
exit;
end;
now:=now^.next;
end;
writeln(-1);
end;
procedure main;
var
ch:char;
i,j,n:integer;
t:longint;
begin
readln(n);
for i:=1 to n do
begin
t:=0;
for j:=1 to 25 do
begin
read(ch);
t:=t*2+ord(ch)-48;
if j mod 5=0 then readln;
end;
print(t);
if i<n then readln;
end;
end;
begin
solve;
main;
end.
======================= 性感的分割线 =======================
Problem : garden / 和MM逛花园
题目来源
07年Matrix67生日邀请赛第四题问题描述
花园设计强调,简单就是美。Matrix67常去的花园有着非常简单的布局:花园的所有景点的位置都是“对齐”了的,这些景点可以看作是平面坐标上的格点。相邻的景点之间有小路相连,这些小路全部平行于坐标轴。景点和小路组成了一个“不完整的网格”。
一个典型的花园布局如左图所示。花园布局在6行4列的网格上,花园的16个景点的位置用红色标注在了图中。黑色线条表示景点间的小路,其余灰色部分实际并不存在。
Matrix67 的生日那天,他要带着他的MM在花园里游玩。Matrix67不会带MM两次经过同一个景点,因此每个景点最多被游览一次。他和他