上次我们谈到，我们考虑时间复杂度时往往假设任意大的整数运算（赋值、四则运算、取余运算、比较运算、位运算包括左移右移）都可以在常数时间内完成，殊不知这留下了一个非常具有研究价值的漏洞：能否利用计算机理想模型中的整数运算，把问题打包成超大整数后并行计算，从而办到一些在普通计算机上无法办到的事情？我们在上一次的文章中介绍了利用“大整数随便算”的漏洞“耍赖”得到了一个线性时间的排序算法。这个漏洞真的已经被充分利用了吗？我们还能从里面榨出多少汁水来？令人无法想象的是，线性时间的排序算法远远没有挖掘到理想大整数运算的巨大潜力，事实上我们能做到常数时间的排序！问题和解答仍然来自Using your Head is Permitted，在这里向Michael Brand表示深深的膜拜。
自然，说“常数时间排序”是有前提条件的，否则即使读入输出也得耗费线性的时间。不过，我们可以假设所有待排序的数都已经打包进一个大整数里，输出时也无需解包，直接返回另一个大整数即可。在这样的情况下，我们完全可以用常数时间完成排序。换句话说，我可以用O(1)的时间，“一下子”就把0100 0111 0001 0010变成0001 0010 0100 0111，不管这个大整数里面装了多少个数。为了方便大家阅读和思考，我们再取一些名字，方便描述。我们把由多个数构成的大整数叫做“整数串”。整数串中所含的数都是二进制，它们用空格隔开。整数串中每个数的位数都必须相等，位数不够用零补足。我们把这个位数叫做“定宽”，本文例子的定宽都是4。
Mathematica
趣题：尽可能用奇数次猜测完成猜数游戏
现在，我在心里想一个不超过n的正整数t。你的任务是尽可能用奇数次猜测猜中这个数（你知道n是多少）。每次猜测后，我都会告诉你你所做的猜测是大了还是小了。你不能猜测已经被排除了的数（来消耗猜测次数），你的每次猜测都必须符合我原来给出的回答。你觉得，你获胜（奇数次猜中）的几率有多大？
动态规划的几个类似的经典模型启发了我们：设a[m]表示采取最优策略后在m个数里猜奇数次猜中的概率，b[m]表示如果题目要求我们猜偶数次，那最优策略下有m个数时获胜的概率是多少。考虑现在我有m个数可以猜，我想在奇数次内猜中。现在我猜的是数字i。狗屎运最好时，我一次猜中直接就赢了，它的概率是1/m；有(i-1)/m的情况下我会得到“大了”的提示，这样的话我需要用偶数次猜测去猜前面那i-1个数；剩余的那(m-i)/m的情况中，我需要用偶数次猜测去猜m-i个数。因此，a[m] = Max {1/m + (i-1)/m * b[i-1] + (m-i)/m * b[m-i], 1≤i≤m} 。类似地，我们也可以得出b[m]的递推公式：b[m] = Max {(i-1)/m * a[i-1] + (m-i)/m * a[m-i], 1≤i≤m} 。
学习使用Mathematica确实是一件好事，你可以用Mathematica非常方便地描述出我们上面的两个递推公式，不需要自己去写那些冗长的程序了。
a[m_] := Max[Table[1/m + (i-1)/m * b[i-1] + (m-i)/m * b[m-i], {i, m}]]; a[0] := 0;
b[m_] := Max[Table[(i-1)/m * a[i-1] + (m-i)/m * a[m-i], {i, m}]]; b[0] := 0;
双向Josephus问题中的分形图形
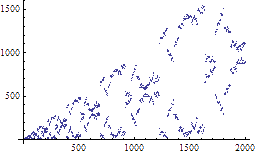Daisuke Minematsu和他的同学们发现，Josephus问题中也隐藏着分形图形。Josephus问题是初学编程的人必然会接触到的一个问题——n个人围成一圈进行1到k报数，每次报到k的人退出游戏（离开这个圆圈），那么最后剩下的那个人是谁。在这里，我们考虑一个Josephus问题的变种：双向Josephus问题。双向Josephus问题中有两个交替进行的报数进程，其中一个按顺时针方向踢出每第k个人，另一个进程则逆时针踢出每第k个人。两个进程交替进行，直到最后只剩一人为止。假如n=10, k=3的话，第一个退出的人是#3，第二个退出的人是#8，第三个退出的人是#6，以后分别是4, 10, 9, 5, 1, 7，最后剩下的人是2。我们用S(n,k)来表示在相应的n值和k值的情况下最后剩下的那个人的编号，对于每个固定的k值，函数S的图象竟然都是一个分形图形。右图是S(n,4)所对应的图象，你可以非常清楚地看到这个图象的自相似性。你可以自己用Mathematica来验证一下。
立体图与三维数据展示
我的左眼有相当严重的散光，因此无缘各种类型的3D立体图，包括看对眼、立体眼镜、左右两幅图（一只眼睛看一个）等等。后来，网上出现了一种只需要一只眼睛就能体验的3D图，原理非常简单，效果也比较震撼。只需要在两个眼睛的位置分别拍照，然后做成gif循环显示两个图片，大脑也可以从中迅速获取信息分辨出第三维来。闲逛ffffound时偶然发现这个图，突然想到：同样的方法为何不用于展示三维数据呢？于是试着用Mathematica做了一个。Mathematica输出gif动画相当简单，只需要一句Export[“file.gif”,{g1, g2, …}]就行了。在这里，我们将用三维空间的点来展示组合数的各位数字之和的分布情况。可以看到，使用3D动画的效果非常明显。
img = ListPointPlot3D[
Table[Total[IntegerDigits[Binomial[i, j]]], {i, 0, 50}, {j, 0, 50}],
ViewVertical -> {0, 0, 1}, ImageSize -> 600];
Export["F:\file.gif", {Show[img, ViewVector -> {-32, -20, 60}],
Show[img, ViewVector -> {-31, -21, 60}]}];
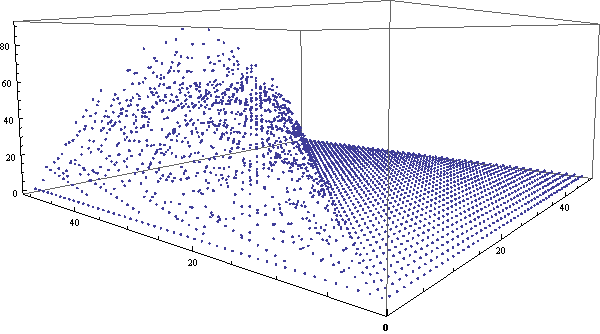
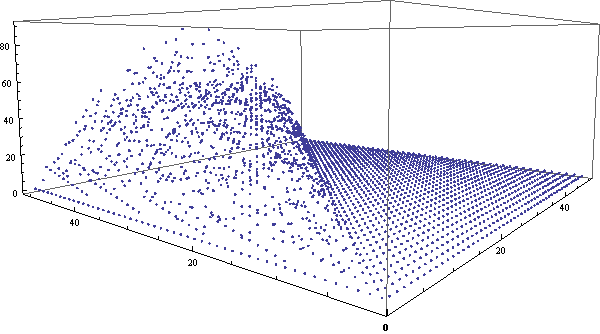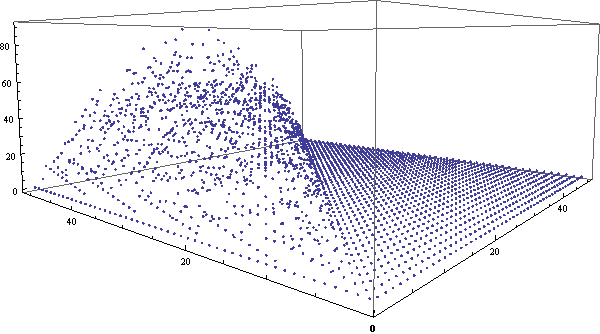
类似地，我们还可以做出环视一周的gif动画来，虽然这样将很难观察出细节，但对总体的把握效果将更好。
牛B的Mathematica：寻找开头和结尾都是字母y的形容词
只有想不到，没有做不到。还是在这里，我惊奇地发现Mathematica居然有DictionaryLookup和WordData这样的函数（我的6.0里就有，不知道5.x有没有）。于是，一连串牛B的Mathematica用法出现了：
包含ijk三个连续字母的单词：
In[1]:= DictionaryLookup["*" ~~ "ijk" ~~ "*"]
Out[1]= {"Dijkstra"}
连续三次出现重复字母的单词：
In[2]:= DictionaryLookup[RegularExpression[".*(.)1(.)2(.)3.*"]]
Out[2]= {"bookkeeper", "bookkeepers", "bookkeeping"}
首尾三个（及以上）的字母完全相同的单词：
In[3]:= DictionaryLookup[RegularExpression["([a-z]{3,})[a-z]*1"]]
Out[3]= {"abracadabra", "anticoagulant", "antidepressant",
"antioxidant", "antiperspirant", "bedaubed", "beriberi", "bonbon",
"cancan", "chichi", "couscous", "dumdum", "entailment",
"entanglement", "entertainment", "enthrallment", "enthronement",
"enticement", "entitlement", "entombment", "entrainment",
"entrancement", "entrapment", "entrenchment", "froufrou", "hotshot",
"hotshots", "ingesting", "ingoing", "ingraining", "ingratiating",
"ingrowing", "ionization", "mesdames", "microcosmic", "murmur",
"muumuu", "outshout", "outshouts", "physiography", "pompom",
"redelivered", "rediscovered", "respires", "restores",
"restructures", "tartar", "tessellates", "testates", "testes",
"tormentor", "tsetse", "underfund", "underground"}